贝叶斯定理：10个让你更厉害的观念

真正的高手，都是贝叶斯主义者。

贝叶斯定理，这个看似简单的公式，有着各种奇妙的运用，不仅好玩儿，还深深影响了我们决策的质量，甚至改变我们的命运。‍‍‍‍‍‍‍

从人生选择，到创业逻辑，再到人工智能，贝叶斯定律可能是对世界影响最大的公式之一。‍‍‍‍

你并不需要太多准备知识，就能完成绝大多数贝叶斯定理的计算。‍‍‍‍

除此之外，这个神奇的定理还给我们带来如下十个观念，彻底改变了我们看世界的方式。‍‍

1. 信念的种子：基础比率的力量

从一个主观的先验概率开始，贝叶斯定理教会我们如何在不确定性中找到希望的起点。

2. 粗略也是一种智慧：行动在不完美中也能美好

贝叶斯分析告诉我们，即使在信息不完全或模糊的情况下，也能做出有力的决策。

3. 流动的信念：持续更新的艺术

贝叶斯思维强调信念不是静态的，而是一个随时间和数据不断更新和适应的动态过程。

4. 简约与全面：奥卡姆剃刀与多维证伪

贝叶斯分析教我们如何在复杂性和简单性之间找到平衡，同时从多个角度审视问题。

5. 因果的新语言：概率作为解释工具

通过贝叶斯分析，我们可以用概率作为一种新的工具来理解和解释因果关系。

6. 知识的三重旋律：经验、探索和更新

贝叶斯思维强调知识是基于经验、通过试探获得，并随着新信息而不断更新的。

7. 智慧的进化：不断逼近真相

贝叶斯方法教会我们如何通过不断的自我修正和更新，逐渐接近真相或最优解。

8. 联结的力量：贝叶斯网络与分布式思维

类似于我们大脑的原理，贝叶斯网络展示了如何通过联结和分布式思维来解决复杂问题。

9. 你的连接定义了你：联结的权重

在贝叶斯世界中，不仅你和谁连接重要，而且连接的“权重”或质量同样重要。

10. 模型的双面性：在相信与怀疑之间寻找平衡

一个贝叶斯主高手，能够在相信中怀疑，在怀疑中相信，并在一个充满不确定性的世界里，持续前行。

一、一道好玩儿的题目

据说是海外某量化巨头的一道面试题：

你有2个预测器，每个预测器在晚上会显示“涨”或者“跌”，来预测明天股市是涨还是跌。

根据历史统计，每个预测器预测的准确率都是0.7，并且预测器之间的预测结果是独立的。

今天晚上，2个预测器，都显示“涨”。

请问：明天股市涨的概率是多少？

第一眼看上去似乎简单，难道不是“1-（1-0.7）的2次方”？

贝叶斯的直觉立即纠正了我。0.7是预测的准确率，而不是上涨的概率。

如果上涨的概率是x，那么预测器A预测上涨的概率是“0.7x+0.3（1-x）”。

正确的计算应该是什么呢？

二、我的手工解答

推理如下。

两个预测器其实是两次独立的信息更新，我们要根据这两次更新的信息来推测“后验概率”。‍‍

题目中是缺先验概率的，所以我们可以毛估估一下，例如估计上涨的概率在40%-60%之间。‍‍‍‍‍‍

为了简便计算，我们假设上涨或下跌的先验概率都是50%。‍

第1步

第一个预测器的预测上涨，其准确率是0.7，于是：

预测上涨并且实际也上涨的概率是0.5x0.7。此谓击中率；‍‍

预测上涨而实际是下跌的概率是0.5x（1-0.7），此谓误报率；

那么我们要的结果就是“击中率/（击中率+误报率）”。

所以，可以计算可能上涨的概率（基于该更新信息的后验概率）是（0.5x0.7）/[0.5x0.7+0.5x（1-0.7）]。

得到的后验概率是70%。‍‍‍‍‍‍‍‍‍

第2步

现在，上面得到的后验概率70%，变成了本次贝叶斯更新的先验概率。‍‍‍‍

第二个预测器的预测上涨，其准确率是0.7，于是：

预测上涨并且实际也上涨的概率是0.7x0.7；

预测上涨而实际上下跌的概率是（1-0.7）x（1-0.7）；

所以，可以计算可能上涨的概率（基于该更新信息的后验概率）是（0.7x0.7）/[0.7x0.7+（1-0.7）x（1-0.7）]。

得到的后验概率是84.48%。

三、按照公式计算‍‍‍‍‍‍‍

如上，是我用零公式法计算了一遍。‍‍‍‍‍‍‍‍‍

我从小懒得记公式，有同学还记得我中学考试时现推公式答对最难的物理题并且得零分。

但公式依然很重要，否则就无法大规模重复。

再有，如果你真正理解了某个公式，你根本用不着记。

我们试着用公式再计算一遍。

首先，我们可以用条件概率来解决这个问题。

记事件A为股市明天涨，事件B为预测器1预测涨，事件C为预测器2预测涨。

已知： 

P(B|A) = P(C|A) = 0.7 （也就是当股市真的涨时，预测器预测涨的概率是0.7）；‍

P(B|¬A) = P(C|¬A) = 0.3 （也就是当股市不涨时，预测器预测涨的概率是0.3）。

我们要找的是P(A|B∩C)，也就是在两个预测器都预测涨的情况下，股市真的涨的概率。

所以，当两个预测器都预测明天股市会涨时，真正涨的概率是约0.845或84.5%。

四、坑爹的基础比率

极少有人会在生活中用贝叶斯定理来计算，但我们经常被其戏弄。‍

下面这道题目，可能是最著名的贝叶斯脑筋急转弯了：

一辆出租车在夜晚肇事后逃逸，而这座城市有红色和蓝色两种出租车，该城市红色出租车占85%。现在有以下信息：

一位目击证人辨认出出租车是蓝色的，当晚警察在案发地对证人的证词进行了测试，得出结论：目击者在当时情况下能够辨认出出租车颜色的概率是80%，错误的概率是20%。

那么，各位读者觉得肇事的出租车是蓝色而不是红色的概率是多少呢？

我最早在一次旅途中看到这道题的。那是一次集体旅行，特别适合在大巴上看书。

可以说，这道题将我带到了一个新世界。

丹尼尔·卡尼曼教授的研究显示，大部分人给出的答案是80%，但正确的答案是41%。

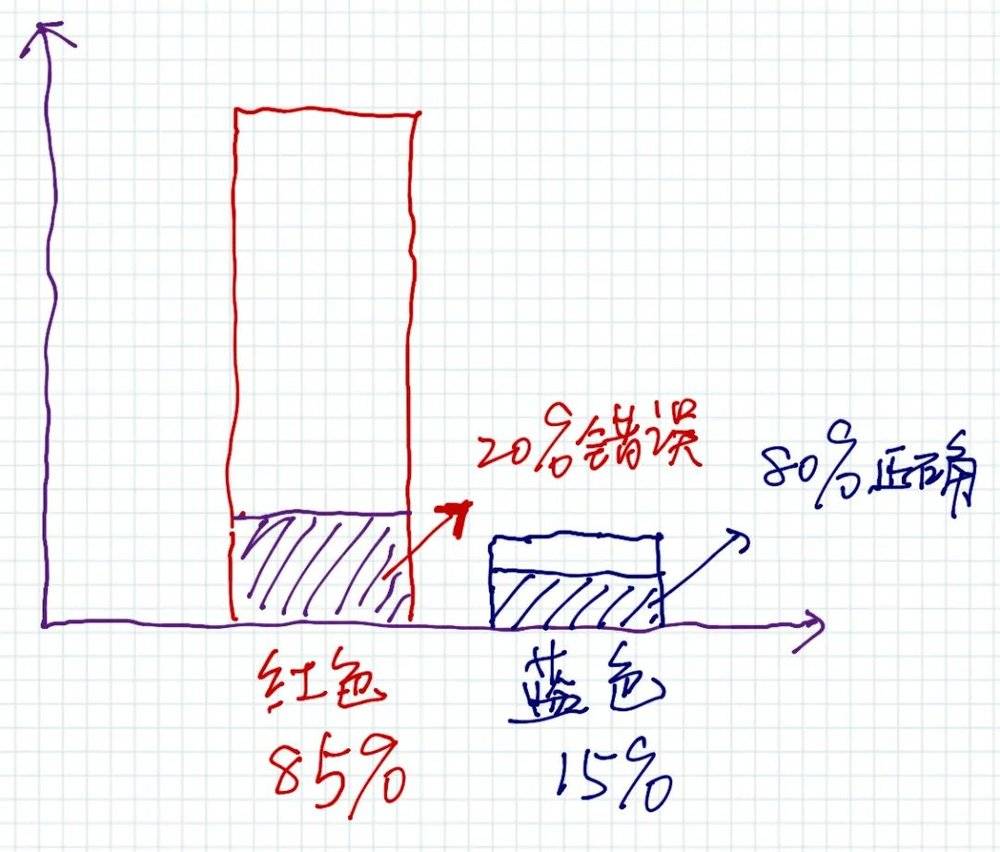
如上图，大多数人忽视了“该城市红色出租车占85%”这个基础比率（基础概率或先验概率在这里是一样的）。

可能性一（误报率）：红色车被误认为是蓝色车的概率是20%，但是红色车的基础比率是85%；

可能性二（命中率）：蓝色车被确认为蓝色车的概率是80%，但是蓝色车的基础概率是15%。‍‍

所以，可能性一大于可能性二。‍‍‍‍‍‍

确切说，我们的大脑不擅长这种拐了一道弯儿的数字游戏。

基础比率往往受到大家的轻视：当人们手头有与该事件相关的具体信息时，很多时候甚至会完全忽视这一比率。

《理性》一书中，举了一个更生动的例子：

佩内洛普是个大学生，朋友认为她冷漠且敏感。她在欧洲旅行过，能说流利的法语和意大利语。

虽然职业规划尚不明朗，但她是一位技艺精湛的书法家，还曾写过一首十四行诗送给男朋友作为生日礼物。

请问：你认为佩内洛普的专业是什么，心理学还是艺术史？

大多数人的第一反应是：当然是艺术史了！

但事实上，13%的大学生主修心理学（不知道是哪里的数据），只有0.08%的学生主修艺术史，几乎是163:1。

所以，佩内洛普更可能是学心理学。

然而，我们先入为主的“刻板印象”，让自己忽视了基础比率的存在。

人们总是追求新奇，追求大招，追求与众不同，然而很不幸，绝大多数人都只是普通人而已。

但这并不是什么坏事，普通人是被基础比率（基础概率）所庇护的。

想想看，在这个看似很糟糕但依然跌跌撞撞运行的世界里，只要我们遵循基本的常识，本分地活着，一般都还不赖。‍‍‍‍‍‍‍‍‍‍‍‍‍‍

问题往往出在我们不愿意平常地活着。‍‍‍‍‍‍‍

这就是为什么“常识”往往很不常见。‍‍

医学界有句格言：“当你听到马蹄声时，想想马，而不是斑马。”

例如，马斯克曾经说过，特斯拉就是要做最好的车。而不是别的什么花里胡哨的概念。这个是某种意义上的第一性原理。

所以，相信阴谋论，相信神医，到处找成功学的偏方，一心憋大招，都是智慧不足的特征。

五、世界的“比率”

卡尼曼的研究里，大量涉及“比例”。

的确，人是一种比例动物，我们对于外部世界的感知，往往是基于比较和变化。

例如，一个人对薪水的满意度，往往不是来自绝对数值，而是来自与同事或同行的对比。

又例如，我们身体感觉的往往是温度变化，而非温度本身。

再复杂一点儿，来看看1964年奥斯本提出的“随机漫步理论”：

他认为股票价格的变化类似于化学中的分子“布朗运动”（悬浮在液体或气体中的微粒所做的永不休止的、无秩序的运动），具有“随机漫步”的特点，也就是说，它变动的路径是不可预期的。

这里特别要强调的一点是：随机漫步的不是股价，而是股价的变化。

让我们说说比率吧。

《数学的雨伞下》讲了个有趣的故事：‍‍‍

作者和朋友玩儿竞猜游戏，问题是地球和月球之间有多远。

作者这组猜是80万千米。另一组猜10千米。

后者的答案显然不靠谱，珠峰就有近9千米，这还不一下子就蹦上月球了？‍‍‍‍‍‍‍‍

然而，结果却是，这个荒唐的答案更接近正确答案。

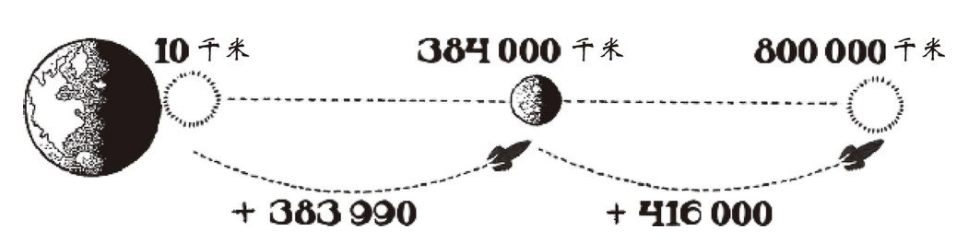
如上图：

1. 月球和地球之间的距离实际上是384000千米；

2. 作者的答案和正确答案差了416000千米；

3. “荒唐组”的答案则只差了383990千米。

所以，看起来更聪明的人反而错得更多！‍‍‍‍‍‍

问题出在哪里？

显然，我们应该计算的是比率，而非加减。

所以，按照比率，用除法计算：

1. 作者组的答案比正确答案大了1.08倍（800000/38400）；

2. 荒唐组的答案只有正确答案的1/38400。

从这个角度来看，作者组遥遥领先。

而且，这个基于比率的结果，更加符合我们对该问题的本能感知。

再说回贝叶斯定理，为什么即使聪明人也容易被绕晕呢？

从上面出租车的例子可以发现：

1. 在除法计算中，分子分母颠来倒去，容易把人绕晕；‍‍‍‍‍‍‍‍‍

2. 具体计算过程中，先除法，再加法，又除法，也容易晕。‍‍‍

说起来，我们还真是像小孩一样，看电影只会问：那人是好人还是坏人？‍‍‍‍‍‍‍‍‍‍‍‍‍

即使再进化一点儿，有些聪明人跳出了非黑即白的二元对立思维，知道用概率来描述灰度，也会在多个概率混杂在一起时犯糊涂。‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍

该话题还可以延伸至“大事不糊涂是追求数量级的正确”的有趣主题上。

再回到贝叶斯定理。

六、用证据更新观念的概率‍‍‍

太多对贝叶斯的讨论，停留在“因漠视基础比率而导致戏剧性后果”这一方面。

而贝叶斯的魔法，更多的来自其“更新”。

平克写道：贝叶斯定理，是控制证据强度的概率法则，告诉我们当知晓了一个新的事实或观察到新的证据时，该如何修改概率（改变我们的想法）。

贝叶斯定理看起来很简单，从头推导也不难：‍‍‍

下图是对公式的直观描述：

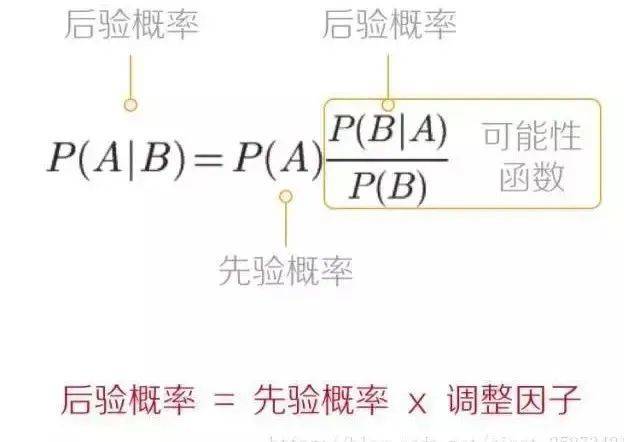
简而言之，就是先有一个“先验概率”，然后根据新的证据更新，得到一个后验概率。

平克用文字描述了贝叶斯定理：

我们在查看“证据”后对“假设”的相信程度，等于我们事先对“假设”的相信程度，乘以“假设”为“真”条件下“证据”出现的可能性，再根据“证据”的普遍程度做出适当调整。

对于贝叶斯更新，更好的数据和信息带来更好的解决方案。

什么是更好的信息？包括且不限于：更多的数据，更靠谱的信息源，更多的角度。‍‍‍‍‍‍‍‍‍

有时候，快速的、有洞见的小数据，可能更有价值。‍‍

贝叶斯更新特别像是一个证伪的过程，所以，更多的不同角度，就像切割钻石的激光。‍‍‍‍‍‍‍‍‍‍

经得起不同角度的奥卡姆剃刀切割的观念，其接近真相的概率更高。‍‍‍‍‍‍‍‍‍‍‍‍

七、厉害的原理‍‍

贝叶斯定理为什么厉害？‍‍‍

贝叶斯定理与人类大脑的推理过程非常相似，所以被称为接近人类感觉的统计学。

在最开始的计算中，我们并没有股市涨跌的先验概率，所以凭主观给出了一个50%的“临时概率”。‍‍‍‍‍‍‍‍

这是一种了不起的毛估估的思路。‍‍

静态角度看，有费米估算的妙趣；‍‍‍

动态角度看，则有在进化中不断逼近真相的智慧。‍

所以，《科学世界》杂志说，贝叶斯统计有一个“不充分推理原则”：若没有其他可作为依据的数据，可以把主观预测当作数据使用。

然后，再根据新的信息，不断更新概率，结果就会越来越准确。‍‍‍‍

本文开始的例子里，两个预测器的准确率都只有70%，但是叠加在一起使用（前提是二者是独立的，现实中很难做到），却可以将预测准确率大幅提升。

所以，贝叶斯定理有一种可以不断重复的杠杆效应。‍‍

举例说，要用贝叶斯定理来识别垃圾邮件。‍‍

根据贝叶斯定理如下：

假设x是垃圾邮件，y是邮件里有“免费”的字眼。计算如下：

可以想象，假如我们继续增加用于证明是垃圾邮件的字眼，会产生叠加效应，大幅提升识别出垃圾邮件的准确率。

（上面案例来自《科学世界》杂志。）

八、贝叶斯的杠杆

让我们通过一个更加直观生动的例子，来感受一下贝叶斯定理的杠杆：

有两个装满大量卡片的盒子，其中一个70%是红色，30%是蓝色；另一个30%是红色，70%是蓝色。 

现在随机选择了一个盒子并取出了12张卡片，其中有8张是红色，4张是蓝色。

那么，请问这些卡片取自第一个盒子的概率是多少？

计算之前，我们根据自己的直觉，随意蒙一下，大概是70%或80%？不妨写下来。

通过贝叶斯计算如下：

通过计算，结果是多少呢？

答案是高达97%。

这个数字比大多数人的估算要高。

毕竟12张卡片里，还有4张是蓝色，来自盒子1的概率为什么高达97%？‍‍‍

这是因为，至少在某些情境下，连续的证据，能够让贝叶斯定理产生某种类似于杠杆原理的逼近速度。

这道题也示范了贝叶斯定理如果根据“果”，来倒推“因”。

我们不断从某个未知的盒子里随机抽出牌，看见“果”。

然后倒推这些牌来自那个盒子，这是“因”。

并且，这些因果并非是传统意义上那种逻辑推理式的，也就是被休谟怀疑的那种脆弱的因果。

贝叶斯定理所描述的因果，是基于主观概率的，并不断在新的证据下更新的信念。‍‍‍‍‍‍

在贝叶斯因子的催化下，我们可以在不确定的世界里，借助有限的信息，持续迭代。

有趣的是，这种看似含混的因果，反而比那些貌似逻辑分明、信誓旦旦的因果更有生命力，更有适应性。‍‍‍

九、贝叶斯更新（案例1）‍‍‍

再说贝叶斯的“更新”。

1968年6月，天蝎号核潜艇在大西洋亚速海海域失踪了，潜艇上的99名海军官兵全部杳无音信。

看起来是不是像大海捞针？

就搜寻的难度而言，的确如此。

海军请来科学家克雷文组织搜寻。

首先，克雷文列出一系列能够解释天蝎号事故的场景。

接着，他组建了一个囊括各方面专家的团队，让每个成员提供自己对每个可能场景的发生概率的猜测。

再而，将各位专家的意见综合到一起，得到了一张20英里海域的概率图。整个海域被划分成了很多个小格子。

每个小格子有两个概率值p和q，p是潜艇躺在这个格子里的概率，q是如果潜艇在这个格子里，它被搜索到的概率。

每次寻找时，先挑选整个区域内潜艇存在概率值最高的一个格子进行搜索。

如果一个格子被搜索后，没有发现潜艇的踪迹，那么按照贝叶斯公式，这个格子潜艇存在的概率就会降低：

如果没有发现，概率分布图则会被“洗牌”一次，搜寻船只就会驶向新的“最可疑格子”进行搜索，这样一直下去，直到找到天蝎号为止。

克雷文采用的正是贝叶斯法，能够利用有限的信息进行预测，并且根据搜索“连续更新”。

（以上案例来自网络。）

也就是说，每一次“没搜到”的遗憾都不会被浪费，也不是简单被标注为“不在这里”，而是用于更新调整整体的估算概率。

十、贝叶斯更新（案例2）

2009年5月31日晚10点，法航447不幸坠毁，搜救人员动用当时最新技术，找了一周后，仅发现少量残骸碎片和29具遇难者遗体。

随后两年的艰苦搜索，更是一无所获。

这时，贝叶斯主义者登场了，他们的方法是：

• 为飞机失事建立一个数学模型；

• 整合评估各种导致失事的原因的概率；

• 根据更新信息，改进模型。

如上，也是一张“格子”图。

救援队根据上述概率分布图，先从概率最大的区域搜索，如果没有发现，就在过往数据基础之上更新概率分布，继续搜索最大概率区域。

其中，贝叶斯更新的过程，简单示范如下：

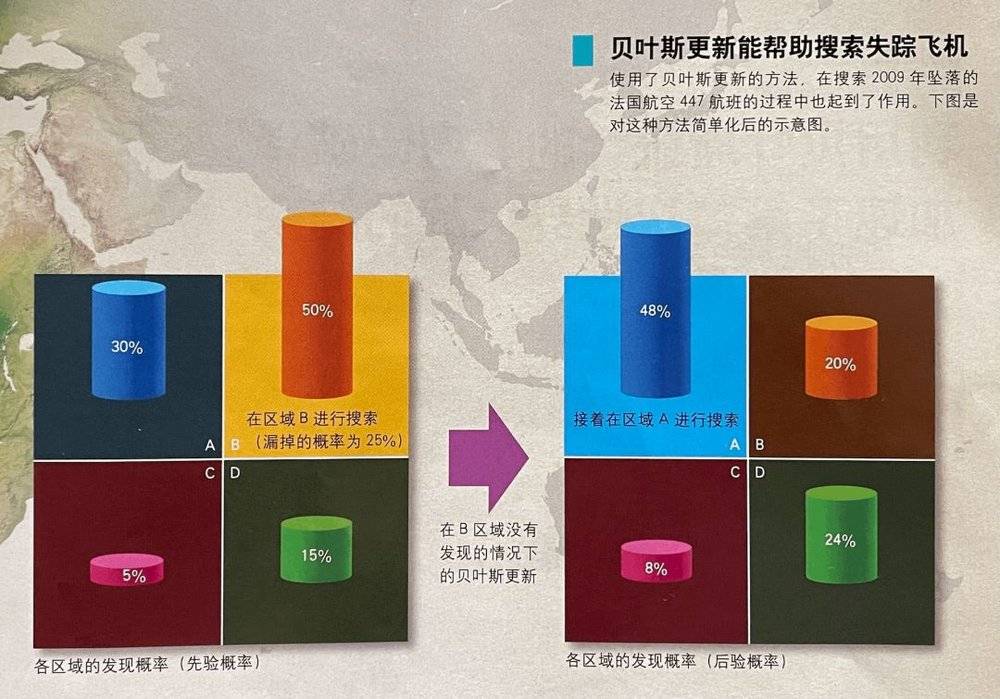
（本图来自《科学世界》杂志）

上面的数字是如何得到的呢？

我试着不用贝叶斯公式，用直观的方式来计算：

在B区域的“初始信念”是50%，搜索之后不在B区域，但是找不到的可能性是：

1. 的确不在B区域；

2. 在B区域但是被漏掉了。

我们假设漏掉的概率是25%（这也是一个信念），于是分析如下：

这里有趣的地方是，对于一个贝叶斯主义者，不仅是“我相信，但我也怀疑我的相信”，甚至于，连我对自己的怀疑也是怀疑的。

假如你知道自己愚蠢，并且能够定义出愚蠢的边界，例如这里“找漏了”的概率之25%，那么该愚蠢就会成为智慧的一部分。

继续上面的不用公式的计算，搜索了B区域，由此更新的信息是：

• 的确不在B区域的概率是37.5%；

• 还是在B区域但是被漏掉的概率是12.5%。

那么，不在B区域的37.5%可能性，就要在ABCD四个区域重新分配，如下图：

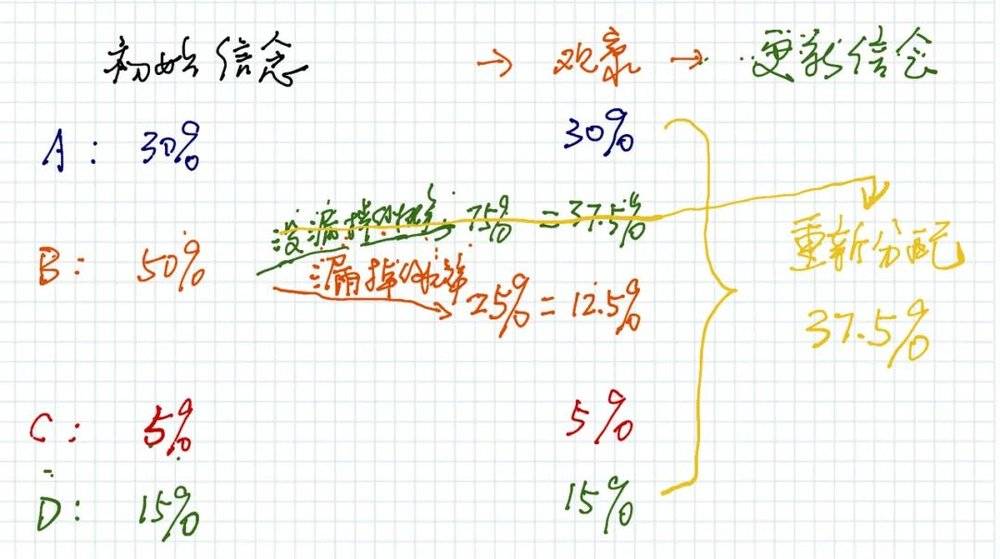
重新分配的基数是（30%+12.5%+5%+15%），以A区域为例，其因为重新分配那37.5%而增加的概率是：

30%➗（30%+12.5%+5%+15%）✖️37.5% = 0.18

于是，更新后A区域的概率是（0.3+0.18=0.48），整体更新后如下图：

这时，A区域的“信念”数值上升为48%，接下来，搜救人员继续搜索A区域。

我们可以想象，假如某个区域的初始信念比较高，并且遗漏概率也比较高的话，即使搜索了该区域而不得，有可能该区域更新后的信念仍然是最高的，所以按照游戏规则仍然是最高的。

历史上的搜救案例里，的确出现过类似的状况，人们根据更新后的数据，重复去搜索此前找过但没找到目标的区域，结果最后找到了。

贝叶斯主义者，将概率理解为对某件事情的信念。

他们承认自己的“信念”是灰度的，而非绝对的判断。

他们会根据观察到的信息更新自己的信念：

• “初始信念”是先验概率，更新后的信念是后验概率。

• 在新一轮的观察中，后验概率又变成初始概率。

我在《人生算法》里的认知飞轮、亚马逊的Day 1、微软的刷新、投资人的打无记忆的球，都是类似逻辑。

贝叶斯推断保留不确定性，每一轮的估算也许是模糊的，然而公式在模糊和犯错的情况下，依然可以发挥作用。

并且，贝叶斯算法具有连续性，可以程序化，以有限的信息，通过某种杠杆效应，快速逼近真相。

当我们添加更多的证据，初始的信念会不断地被“洗刷”。

有人把天蝎号潜艇案例视为“群体智慧”，也有人将其视为“试错法”，其实并不精确。

贝叶斯法，每一次都能利用新信息（哪怕是失败的信息），对原有信念进行更新。

这就是杠杆作用。

更重要的是，这一过程可以不断循环，连续作用，从而产生了指数效应。

所以，贝叶斯思维的杠杆，是一种关于“可能性”的杠杆。

十一、朴素贝叶斯

贝叶斯定理厉害，还因为算法与AI。‍‍‍

再看一道题：‍‍‍

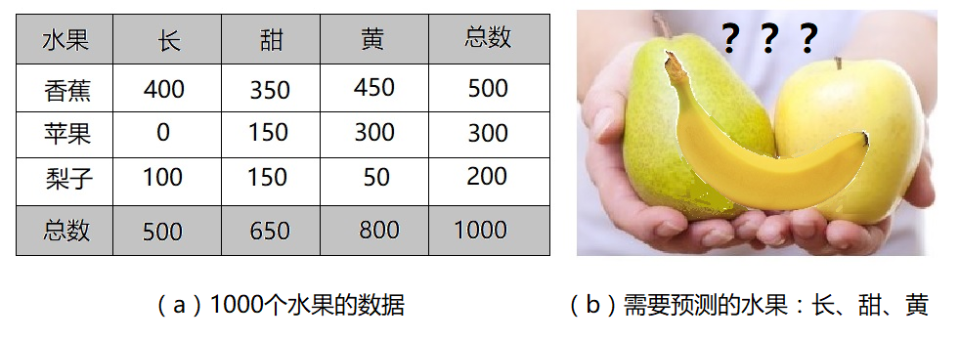
如上图。我们测试了1000个水果的数据，包括如下三种特征：形状、味道、颜色，这些水果有三种：苹果、香蕉、或梨子。

请问：如果某水果的特征是“长、甜、黄”，请问该水果是哪一种？

简单分析如下。‍

从数据中，我们知道：

1. 这些水果中，50%是香蕉，30%是苹果，20%是梨子。也就是说，P（香蕉） = 0.5，P（苹果） = 0.3，P（梨子） = 0.2。

2. 500个香蕉中，400个（80%）是长的，350个（70%）是甜的，450个（90%）是黄的。也就是说，P（长|香蕉） = 0.8，P（甜|香蕉） = 0.7，P（黄|香蕉） = 0.9。

以此类推，我们可以分别计算出别的条件概率。

接下来，要计算的是，在“长、甜、黄”这一特征信息的“更新”之下，某水果是苹果、香蕉、或梨子的概率。

以计算香蕉为例，“长、甜、黄”的条件下是香蕉的概率是：‍‍‍

P（香蕉|长甜黄） = P（长甜黄|香蕉）P（香蕉）/ P（长甜黄）

其中，是香蕉的条件下，符合“长、甜、黄”的概率是：

P（长甜黄|香蕉）  = P（长|香蕉） * P（甜|香蕉） * P（黄|香蕉） = 0.8*0.7*0.9 = 0.504。

再以同样方式，分别计算P（长甜黄|苹果） ，P（长甜黄|梨子） 。接下来：

P（长甜黄） =  P（长甜黄|香蕉） P（香蕉） + P（长甜黄|苹果） P（苹果） + P（长甜黄|梨子） P（梨子）

于是，我们可以计算出来：P（香蕉|长甜黄）= 93%

上面的计算从数学的角度看非常简单，从人类理解外部世界的常识来看也无非如此，但绕在一起却很容易让人犯晕。

一个直观的描述来自 3Blue1Brown的讲解，如下图：

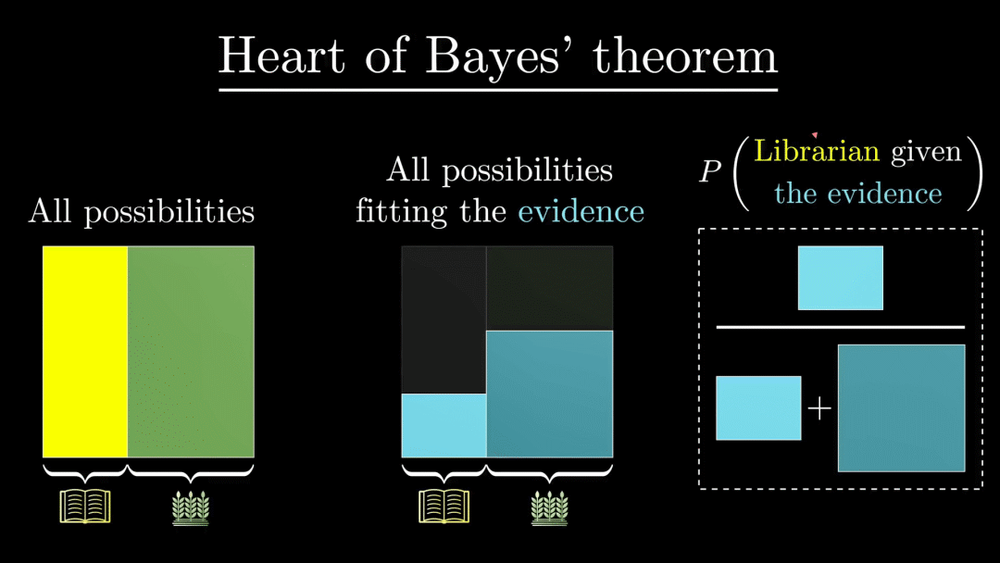
1. 假设我们有两种水果，如上图左侧，分别是香蕉和苹果。‍

2. 上图中间，则是香蕉和苹果分别符合“长、甜、黄”这一特征的概率。‍‍‍‍

3. 上图右侧，则是计算符合“长、甜、黄”这一特征的水果是香蕉的概率。‍‍

呃，很直观吧。

从上图中，我们再次感受到，贝叶斯定理是一种关于比例的表述。

如果我们用一种可视化的方式来建模，就不会那么容易因为分子和分母的变换而被绕晕。

这是一个朴素贝叶斯计算。

朴素贝叶斯假设了样本的每个特征之间是互相独立、互不影响的。

例如在上面的题目里，认为“长、甜、黄”这些特征都独立地贡献了这个水果是一个香蕉的概率。

然后，通过应用贝叶斯法则来“合并证据”。

这种假设关系太过于理想，所以这也是朴素贝叶斯的”Naive”之处。

《人工智能：现代方法》写道：

朴素贝叶斯模型有时被称为贝叶斯分类器（Bayesian classifier），这种有点粗心的用法已经促使真正的贝叶斯学派称其为傻瓜贝叶斯（idiot Bayes）模型。

在实践中，朴素贝叶斯系统通常表现得很好，即使条件独立性假设并不是严格成立的。

该书提及：‍‍即使是看似复杂的问题，也可以用概率论精确地表述出来，并用简单的算法求解。

很多时候，尤其是在一个不可避免的不确定世界里，概率比逻辑做得更好。

十二、经验主义

根据特征识别水果的例子，让人想起了洛克。

洛克认为人心中没有天赋观念，“人心就如一块白板”（Tabula Rasa），一切知识和观念都起源于经验。

“人们能够经验外界事物，并对所观察的事物加以反省，我们便得到知识。”

例如，我们对香蕉的认知，来自我们的经验，如下图：‍

洛克认为观念是思维的对象，感觉和反省是观念的两大来源，合称为经验。

感觉（sensation）：物刺激感官，感官被动地产生观念。例如：黄、白、热、冷、软、硬、苦、甜，以及一切所谓可感物。

反省（reflection）：我们的心灵主动地反省自身内部的心理活动。例如：知觉、思想、怀疑、信仰、推论、认识、意欲，以及人心的一切作用。

洛克还提出了“第一性质与第二形式”和“简单观念与复杂观念”等理论，例如：我们唯一能感知的是简单观念，而我们自己从许多简单观念中能够形成一个复杂观念。

就像人类，或者人工智能，在信息不充分的环境里，根据“长、甜、黄”等简单观念所提供的证据，合并在一起，推测出一个相对复杂的观念。‍‍

洛克和别的一些哲学家天才般的朦胧奇思妙想，为后来的贝叶斯主义者和人工智能都埋下了火种。

随后的故事非常有趣：

经验主义者洛克影响了怀疑主义者休谟；

而牧师贝叶斯则试图反对那些对上帝不敬的家伙，结果提出了贝叶斯定理，为经验主义和怀疑主义献上了一大神器；‍

从此，人类可以在经验和怀疑的迷雾中，以贝叶斯定理为拐杖前行。

如今，经验主义已经超越了哲学家的杠精式的讨论。

在科学领域，经验主义强调证据，尤其是在实验中发现的证据。

“所有假设和理论都必须根据对自然世界的观察进行检验，而不是仅仅依赖于先验推理、直觉或启示，这是科学方法的基本组成部分。”

在本文的语境里，我偏向于自然科学学者经常使用的经验主义：

1. 知识是基于经验的；

2. 知识是试探性（tentative）的和概率性的，会不断被修正和证伪”；

3. 以经验（或观察）为依据的研究，包括实验和经过验证的测量工具，指导科学方法。

贝叶斯定理整合了“过去经验”、“新的证据”和“修正后的判断”，提供了一种将新观察到的证据和已有的经验结合起来进行统计推断的客观方法。

十三、经验主义 VS 理性主义

ChatGPT的胜利，让很多人感慨，经验主义再次将理性主义甩到了后面。

这里的理性主义，是一个相对狭义的概念。

在人工智能的范畴里，经验主义和理性主义研究范式交替出现，二者对比如下：

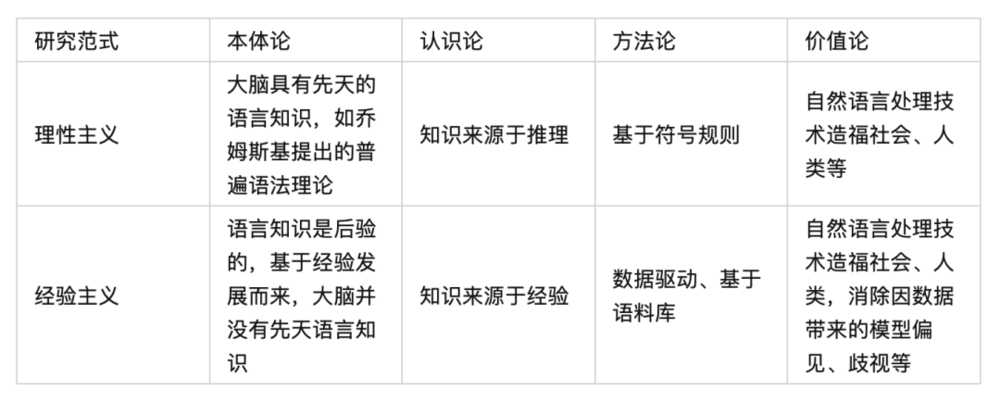
来自《从ChatGPT看“自然语言处理之经验主义与理性主义”》‍

理性主义的领军人物乔姆斯基应依然在世，今年（2023年）近九十五岁。

他在《纽约时报》上撰文《 ChatGPT的虚假承诺》，用了一个例句：John is too stubborn to talk to。

乔姆斯基认为机器会把这个句子理解为：John太固执不愿意和人谈话；

而不会正确地理解其本意：John不可理喻。

然而，当人们将问题抛给ChatGPT，发现ChatGPT能够准确地知道这个句子的深层含义。‍‍‍‍‍

克拉克定律再次显灵：

如果一个年高德劭的杰出科学家说，某件事情是可能的，那他几乎就是正确的；但如果他说，某件事情是不可能的，那他很可能是错误的。‍

斯坦福大学的计算语言学家克里斯·曼宁说：

“看到一位年轻时深刻的创新者，现在却保守地阻碍激动人心的新方法，真是令人悲伤。”

但是，在我看来，这位年近百岁的斗士在科学上最后的固执，可能是他可以作出贡献的最好形式。毕竟ChatGPT已经足够热了，不需要一个附庸的老家伙。‍‍

在电影《模仿游戏》里，图灵炒掉了语言学家；‍‍

费曼总是在嘲笑哲学家；‍‍‍‍‍‍‍

塔勒布也调侃说“我们从来不认为鸟类学会飞行得归功于鸟类学家的成果”。

但是有研究人员认为自然语言处理的发展需要理性主义与经验主义共同推进，尤其需要语言学理论、语言学知识支撑。

理由是：语言学家研究语言现象，就像物理学家研究物理现象，正如工程师需要物理洞见，自然语言处理研究人员的任务就是研究如何使用语言学洞见。

如上讨论有含混之地，我分别从两头替双方辩护一下，例如：‍‍

1. 塔勒布嘲讽鸟类学家不能教会鸟学会飞行，但是物理学家可以教会飞机飞行；

2. 语言学之于自然语言处理，到底是鸟类学家，还是物理学家呢？

不管怎样，一种稳妥的方法是，综合逻辑和概率，正如贝叶斯定理所表现出来的包容性。

贝叶斯定理最根本的结论之一就是：

新证据不能直接凭空的决定你的看法，而是应该更新你的先验看法（之前的经验）。

我赞成平克在《理性》一书中对“理性”概念的拓展：‍‍

理性不是说知道事实，而是认识到哪些因素是有关的。

十四、证据叠加

《终极算法》提及了一个难题：

假设你在读《纽约时报》，讲的是外星人已经登陆地球。

这一天不是4月1日，可能这是一个玩笑？

但是现在你在《华尔街日报》《今日美国》《华盛顿邮报》看到一样的标题。

你开始感到慌张。但是，如果你查看细节，会发现这四家报社都从美联社那里得到这个新闻标题，你又返回去怀疑这是一个玩笑，而这次开玩笑的是一位美联社的记者。

规则系统无法解决这个问题，朴素贝叶斯法也一样。

这个问题，涉及到证据的不独立性和信息的重复计算。

在贝叶斯推理和朴素贝叶斯分类器中，这是一个常见的问题，通常称为“证据叠加”。

在本文以上的诸多计算中，我们总是在强调证据的独立性。

在本节案例里，如果所有的信息都来自同一个源（在这里是美联社），那么即使多个报纸都报道了这个事件，这些证据也不应该被视为独立证据。

在思考这类让人疑惑的难题时，我们应该学会提问：还有哪些可能的潜在变量？

我试着让ChatGPT来描述一下：

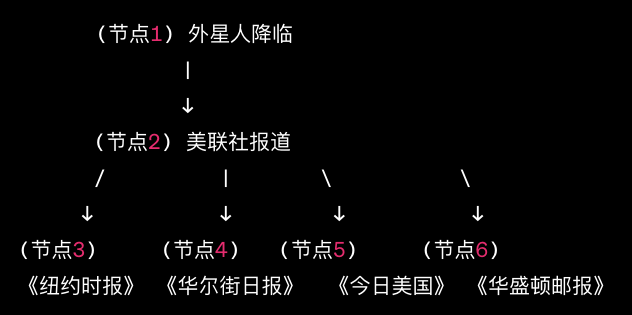
如上图：

1. 从节点1到节点2的箭头表示外星人降临（或没有）会影响美联社是否报道；

2. 从节点2到其他各节点的箭头表示美联社的报道（或没有报道）会影响其他报纸是否报道这个事件。

我们可以得知，如果所有的信息源都来自美联社报道，那么不管在节点2之下延伸出多少子节点，也不能作为更多证据来放大外星人降临的可能性。‍‍‍‍

贝叶斯定理很强大，但前提是模型必须正确地捕捉到关键变量之间的关系。

如果模型过于简单或者没有考虑到这些依赖性，就可能出现问题。

上面那张简陋的图，就是一个贝叶斯网络。

十五、贝叶斯网络（之一）

假设你是一位侦探，收到一个神秘的任务：找出邻居家草地为什么会湿润。经过一番调查，你发现只有两个可能的“嫌疑人”：

1. 下雨（R）：也就是说，是不是老天爷在搞鬼？

2. 喷水装置打开（S）：或者是不是家里的自动喷水装置搞的鬼？

在这个情境中，有三个随机变量：

1. R（下雨）：是否下雨

2. S（喷水）：喷水装置是否打开

3. W（湿润）：草地是否湿润

这三个随机变量的关系可以用一个有向无环图来表示如下：

在这个网络中，节点R和节点S是因节点，而节点W是被影响节点。

贝叶斯网络是一种用于表示变量之间条件依赖关系的概率图模型。它通过有向无环图来表示这些关系。

在上图中，节点代表随机变量（它们可以是可观察到的量、未知参数或假设等），而有向边则表示一个变量可能如何影响另一个变量。

20世纪70年代末，人工智能领域针对如何处理不确定性因素展开了激烈讨论，各种主张层出不穷。

在1982年，“贝叶斯网络”之父朱迪亚·珀尔提出了一个表面上平淡无奇但实际上非常激进的建议：

将概率视作常识的“守护者”，聚焦于修复其在计算方面的缺陷，而不是从头开始创造一个新的不确定性理论。

更具体地说，我们不能再像以前那样用一张巨大的表格来表示概率，而是要用一个松散耦合的变量网络来表示概率。

贝叶斯网络有如下特点：

1. 条件依赖性：贝叶斯网络通过图的形式表达了条件依赖关系。如果一个箭头从A指向B，那么B在一定程度上取决于A。

2. 概率性：每一个节点都有一个条件概率表，用于描述给定其父节点状态下该节点状态的概率。

3. 推理与学习：给定一部分节点（观测数据），你可以使用贝叶斯推断来估算其他未观测节点（隐藏变量）的概率分布。

贝叶斯网络的强大之处在于，即使在复杂和不确定的情况下，它也能提供一种逻辑严谨的方式来推断未知变量的概率分布。

十六、贝叶斯网络（之二）

再来一题。

你可能也经历过在机场等行李的煎熬。假设如下状况：‍‍‍‍‍‍‍

1. 行李丢掉（没上飞机）的概率是50%；‍‍‍‍‍‍‍‍‍

2. 行李的等候时间为10分钟（并且是均匀的）；

请问，等了5分钟之后，还没看到行李，那么你的行李没被弄丢的概率是多大？

方法一：不靠谱的直觉

首先，用直觉快速解答一下：

假设行李没掉，概率是50%，目前还有5分钟，也就是还有50%机会等到行李，那么是不是应该是（50%✖️50%=25%）呢？

然而，这个解答是错的。

方法二：贝叶斯定理

我们可以按照以下方式使用贝叶斯定理来计算这个问题。

首先，我们定义以下几个事件：

正确答案是：1/3。‍

上面两个计算中，第一个直觉上的错误非常有趣。‍‍

没错，假如用平行宇宙的思考方式，很容易想到25%的可能性。‍‍

但是，概率所描述的未知，在经历了5分钟的等待之后，基数已经变成（25%+50%）了，所以计算结果应该是[25%➗（25%+50%）]。‍

为什么在经历了5分钟之后，在行李没丢的那一半平行宇宙被压缩到了25%，而行李丢了的那一半平行宇宙还是按照50%来作为基数呢？‍‍‍‍‍‍‍‍‍‍‍‍‍‍

这是无聊但好玩儿的思考，你不妨在大脑里模拟一下。

不过，这一节的重点是贝叶斯网络。‍‍‍‍‍‍‍

在《为什么》一书里，朱迪亚·珀尔用上面这个例子，来讲解他的理论。‍‍‍‍‍‍‍

为了让人们更加直观地理解，他首先绘制了一个因果图：‍‍

为了将因果图转化为贝叶斯网络，我们必须指定条件概率表，下图是为解决“行李箱在传送带上”的概率这一问题创建的条件概率表：

借助于这个例子，朱迪亚·珀尔强调：

即使上面这个例子只是一个有3个节点的小型网络，它仍然包含2×11=22个父状态，且其中的每一个都为子状态的概率做出了贡献；

如果一个节点有10个父节点，且每个父节点都有2个状态，则条件概率表将超过1000行；

如果10个父节点中的每一个都有10个状态，那么这张表将有100亿行！

《为什么》一书写道：

“为此，人们通常会对网络中的连接进行筛选，只保留那些最重要的连接，让网络保持一个相对“稀疏”的状态。

在贝叶斯网络的发展过程中，其中一项技术成果就是开发出了一种方法让我们可以利用网络结构的稀疏性实现合理的计算时间。”

十七、贝叶斯网络（之三）

能看到一个理论的创造者介绍自己的灵感从何而来，是一件令人愉悦的事情。

朱迪亚·珀尔说自己的灵感来自大卫·鲁梅哈特的一篇文章。

“大卫·鲁梅哈特是一位认知科学家，也是神经网络的先驱。他在1976年发表的关于儿童阅读的一篇文章中明确指出，阅读是一个复杂的过程，其涉及许多不同层次的神经元同时发挥作用。”

他介绍了一个层次化的框架，通过这个框架，不同层次的神经元负责解决不同级别的问题，然后将信息向上传递。

让我们以阅读为例：

1. 字母层面：识别个体特征，如线条和曲线，判断它们可能构成哪个字母；

2. 词汇层面：根据识别的字母和字母组合猜测可能的词；‍

3. 句法层面：根据猜测的词和语法规则进行进一步的推断；‍

4. 语义层面：考虑上下文信息，对整个句子或短语进行解释。

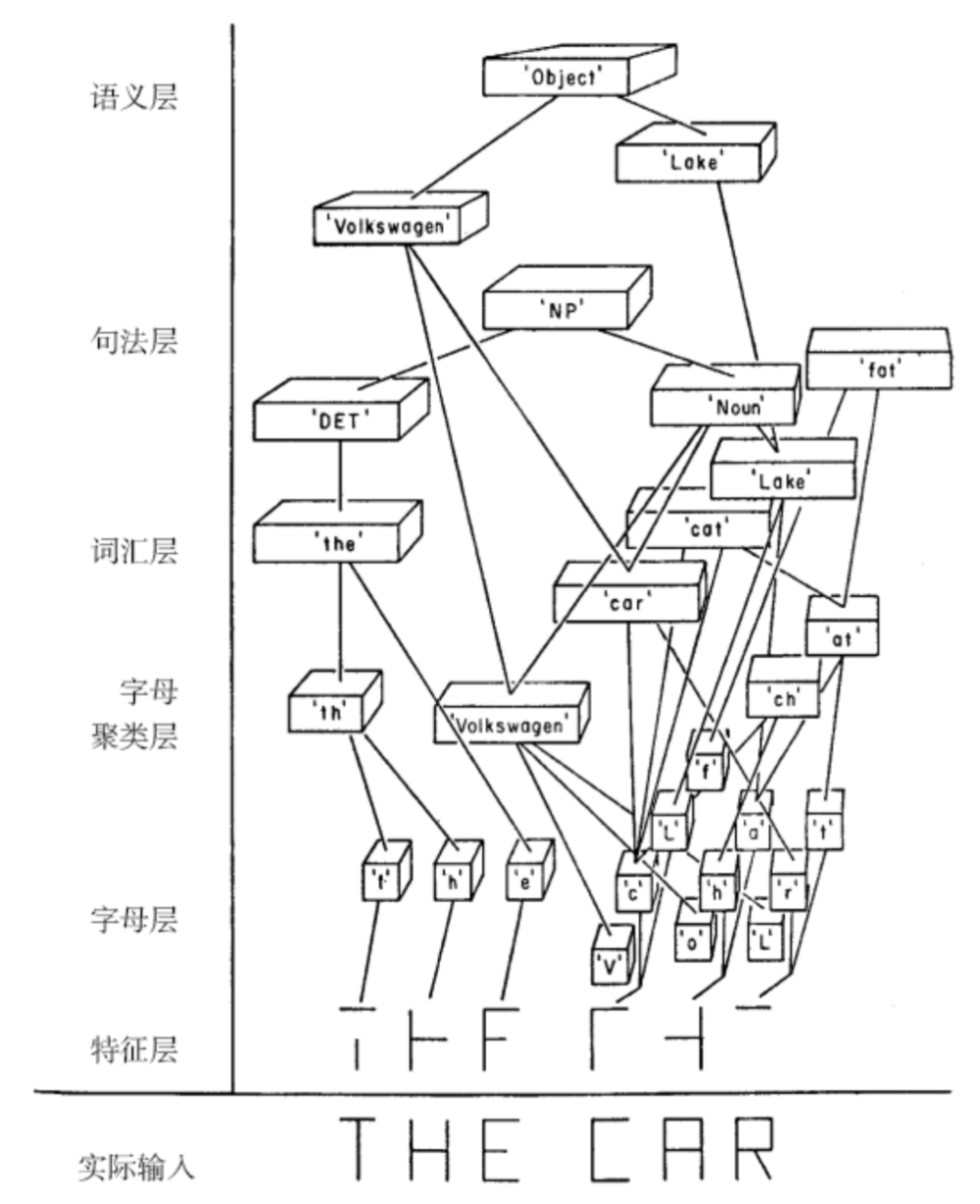
大卫·鲁梅哈特的神经网络草图

上图表明了我们大脑的信息传递网络是如何学会识别短语“THE CAR”的：

1. 在字母层面上，它可能是“FHP”，但在词汇层面，这个字母串是没有意义的。

2. 在词汇层面上，这个词更可能是“FAR”、“CAR”或“FAT”。神经元将这些信息向上传递到句法层面，我们因此判断出在“THE”之后出现的应该是一个名词。

3. 最后，这些信息被传递到语义层面，我们进而意识到因为前一句提到了大众汽车，所以这个短语很可能是“THE CAR”，代指同一辆大众汽车。

更关键的是，上图中我们可以发现：

“所有的神经元都是同时来回传递信息的，自上而下，自下而上，自左向右，自右向左。”

这意味着，大脑是一个高度并行的系统，而非过去我们认为的是一个单一的、集中控制的系统。

朱迪亚·珀尔从鲁梅哈特的论文中认识到：

任何人工智能都必须建立在模拟我们所知道的人类神经信息处理过程的基础上，并且不确定性下的机器推理必须借助类似的信息传递的体系结构来构建。

然而，难题是：信息具体指的是什么呢？

想了好几个月，朱迪亚·珀尔终于认识到：信息是一个方向上的条件概率和另一个方向上的似然比。

更进一步，他将贝叶斯定律和神经网络的推理结合了起来。

朱迪亚·珀尔认为：

1. 网络应该是分层的，箭头从更高层级的神经元指向较低层级的神经元，或者从“父节点”指向“子节点”。

2. 每个节点都会向其所有的相邻节点（包括层次结构中的上级节点和下级节点）发送信息，告知当前它对所跟踪变量的信念度（例如，“我有2/3的把握认为这个字母是R”）。

3. 接收信息的节点会根据信息传递的方向，以两种不同的方式处理信息。

4. 如果信息是从父节点传递到子节点的，则子节点将使用条件概率更新它的信念。

贝叶斯网络中的每个节点（变量）通常只与其父节点和子节点有直接的依赖关系，这大大减少了需要考虑的变量数量和相应的计算负担。

故事的另外一条主线，顺着神经网络前行。

1986年10月，大卫·鲁梅尔哈特、杰弗里·辛顿和罗纳德·威廉姆斯发表了《Learning representations by back-propagating errors》。

该论文描述了一种新的学习程序，可用于神经元样网络单位的反向传播，其掀起的惊人浪潮，正是当下大热的深度学习。‍‍‍‍

必须一提的是，朱迪亚·珀尔试图将因果引入概率世界。而在神经网络原教旨主义者辛顿看来，许多类似的主张完全是多余的。‍‍‍‍‍‍

十八、最后

本文从一道有趣的题目开始。‍

顺着一道题，我又做了另外几道题，顺便温习了一些自己从没主动记过的公式。希望我可能出现的错误别太离谱。‍‍‍‍

很遗憾的是，当我试图找到一些相关例题时，发现在网络上极其匮乏，例如搜索“贝叶斯网络”，排在前面的文章不仅重复，还是错的。‍‍‍‍‍‍‍‍‍

所以我自娱自乐地将一些典型的贝叶斯定理的案例，都从头演算了一遍，并试图从可感知的角度，探寻其神奇力量的“为什么”。‍‍‍‍‍‍‍‍‍‍‍

文章太长了，我来不及写贝鲁的Turbo码，其核心思想也是贝叶斯网络：

通过两个不同编码过程对单一信息进行编码，从而提供多个独立（或近似独立）的观察结果。

这里的关键词，也是“独立”。所以，说起一个人的独立思考，不仅是自己与他人的相对独立，甚至也包括自己与自己的相对独立。

确切说，本文是一场好玩儿的智力游戏。

我只想搞懂到底为什么。要做到这一点，我们需要从数学、哲学、物理、生物学、信息学的角度去切入问题的本质，而不是简单地套用公式。

用自然科学隐喻人生道理，大多数时候都是胡说八道。本文目的亦不在此。

贝叶斯定理有一种奇怪的乐观主义精神，教我们在未知中前行。‍‍‍‍

在生活中，很多时候，那些看上去疑虑重重的人也许有更坚定的信念，而那些信誓旦旦的家伙每每总是见利思迁。

贝叶斯主义假设“现实”的所有模型、理论和概念都不过是某种信念。

这并不会令人成为虚无主义者，反而更能够令我们在相信中怀疑，在怀疑中相信。‍

“所有的模型都是错的，有些模型很有用。”

这个世界很混蛋，但竟然如此刚刚好够我们生存；‍‍‍‍‍‍这个星球很残忍，却总能给我们留下一扇门。

未知令人恐惧。但是，假如希望不是以概率化的方式呈现，又算得上什么希望呢？‍‍‍‍‍‍‍‍

你看，你我都可以有自己的主观信念，带着些许模糊，在这个不确定的世界里，伴随着我们不必抛弃的好奇心，如孩子般前行。

本文来自微信公众号：孤独大脑 （ID：lonelybrain），作者：老喻