如何用数学思维，理解商业世界的底层逻辑

我常说，只有底层逻辑才有生命力。

因为底层逻辑在面临变化的时候，能够应用到新的变化里面，会产生出新的方法论。

只有掌握了底层逻辑，只有探寻到了万变中的不变，才能动态地、持续地看清事物的本质。

可是你相信吗？

在这个世界上，其实有这么一样东西，天生就是一种“底层逻辑”。

那就是，数学。

数学，是用来描述万物本质的语言，是理解这个世界的底层逻辑。只有从数学上理解了一件事情，你才真正从本质上理解了这件事情。

经济学的尽头，是数学；物理学的尽头，是数学；所有自然学科的尽头，都是数学。

而商业和数学，也有着令人惊叹的紧密联系。

看似复杂的商业模式，用一个简洁的数学公式便可揭示其奥妙。很多棘手的商业问题，利用一些简单又常见的数学知识就能找到解法。

这就是我在《底层逻辑2》里，最想与你分享的：如何用数学思维，理解商业世界的底层逻辑。

在这本书里，我想和你分享6种和商业高度相关的数学知识：

1. 四则运算

2. 笛卡尔坐标系

3. 指数和幂

4. 方差与标准差

5. 概率与统计

6. 博弈论

希望这些数学知识，能为你带来洞察之眼、深思之心，让你看透商业的本质，在商业世界里走得更远，飞得更高。

但是，我知道，我理解，我都懂。

数学，可能也伤害过你。

但请相信我，作为数学专业的毕业生，我可以很负责任地说，数学一点都不难。

而且，每一个数学逻辑，都能解决无数现实问题。

什么？你还是不信？

好吧，那我给你举个例子吧。

一、数学有趣，而且有用

先抛一个问题。

请口算，9乘以13，等于多少？

117？没错。怎么算的？

是不是先脱口而出“三九二十七”，然后用27加90，得出了117？

是的。我也是这么算的。这没错。

但是你发现没有，这么算有个步骤，是你绕不过去的，那就是“三九二十七”。

可是，你是怎么知道“三九二十七”的呢？

因为你和我一样，小时候背过“九九乘法口诀”。

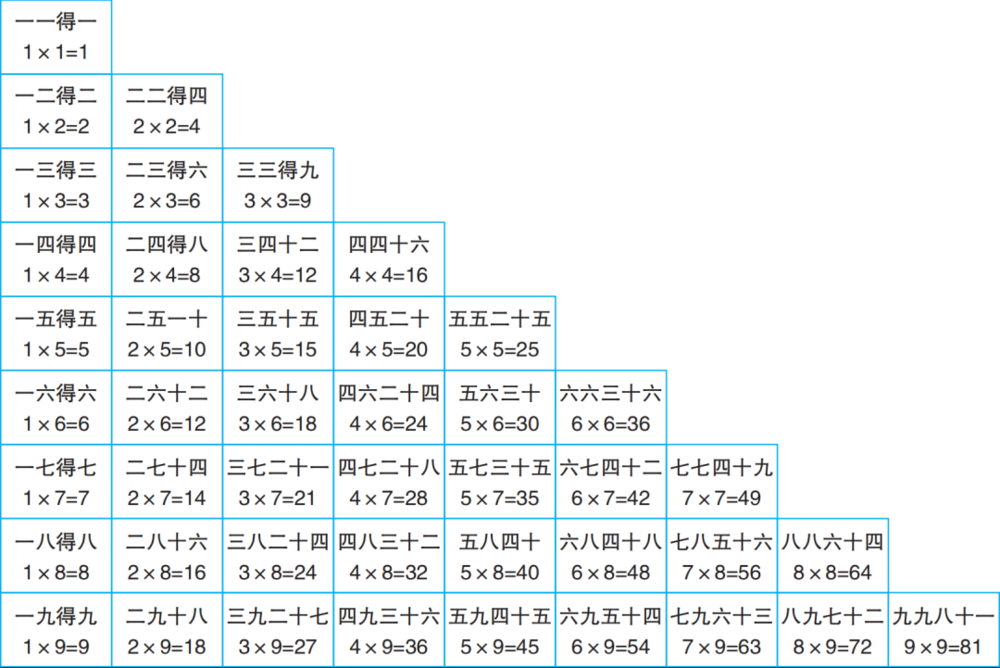
我们所有关于乘法的计算，都是建立在熟练背诵九九乘法口诀的基础上。

但是，你知不知道这个世界上，有一些国家，是不背九九乘法口诀的呢？

你不信？那你问问你周围的俄罗斯朋友。

这个战斗民族，就是不背九九乘法口诀的。

事实上，全世界靠背诵“九九乘法口诀”来做乘法口算的国家，主要都集中在东亚。

比如中国、日本、韩国、越南。

而俄罗斯、法国等很多国家，都没有“九九乘法口诀”。

太不可思议了吧？没有九九乘法口诀，那他们怎么做乘法呢？

他们的乘法，五花八门，很开脑洞。但是都是有用的。

比如俄罗斯。俄罗斯人，是怎么计算9乘以13的？

俄罗斯人会拿一张纸，把9和13，分别写在第一行的左边，和右边。然后，在第二行，把9翻倍（18），把13减半（6.5）。6.5不是整数，就舍掉小数，只写6。所以第二行就是18和6。同理，第三行把18翻倍，把6减半，就得到36和3。第四行，再翻倍和减半，就得到72，和1.5。1.5扔掉小数，当1用。于是第四行，就是72和1。

听上去有点复杂，画张图就明白了。

然后呢？

然后你看看右边这一列，有哪几个是“奇数”。13，3，1，这三个都是奇数。

那么就把这三个奇数左边的数加在一起看看是多少？

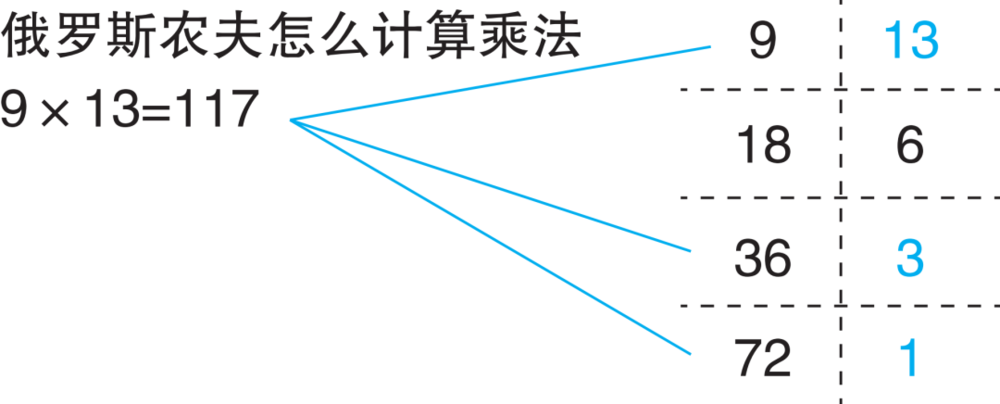
没错。就是117。

天啊，这也太神奇了吧？就这么不断的左边翻倍，右边减半，最后把其中几行一加，就是正确答案？为什么啊？

今天我们不讲为什么。今天就是想告诉你，乘法，其实不止一种。

这种乘法，就是俄罗斯乘法，又称“农夫乘法”。

它的计算效率不如九九乘法口诀高。但是，也是准确而有用的。

数学，准确而有用，就是对的。

再比如古埃及。古埃及人的乘法，很有意思。9乘以13，怎么算？

公元前3000年，古埃及人是用堆石头的方式来计算乘法。

他们先在地上堆13个石头。然后在右边另放一个做标记。第二行的石头翻倍，标记也翻倍。第三行在第二行的基础之上再翻倍。第四行再翻倍。

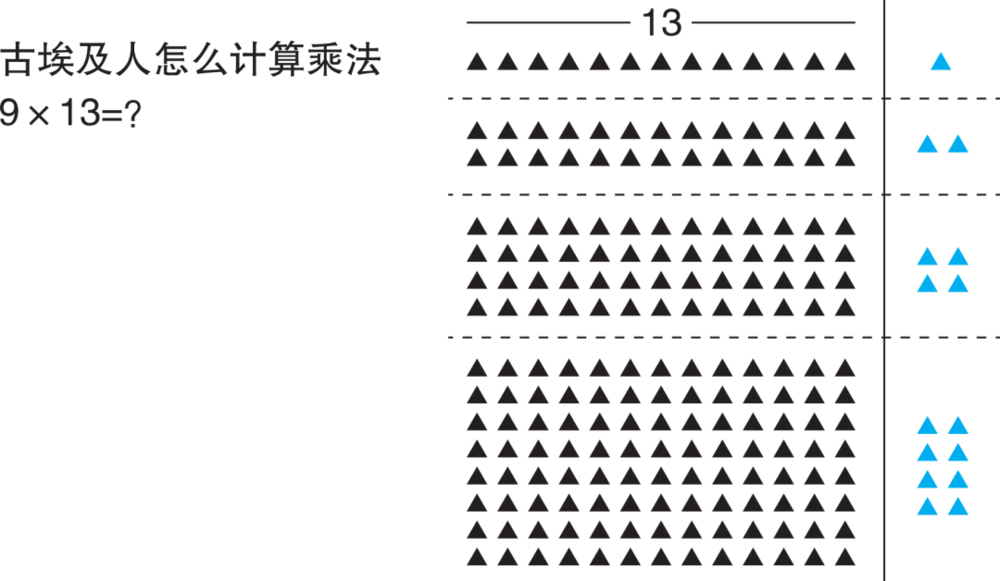
现在我们看看右边用于标记的石头，哪几行加在一起是9个？

第一行和第四行？好的。把这两行的石头加在一起数一数。看看有多少个？

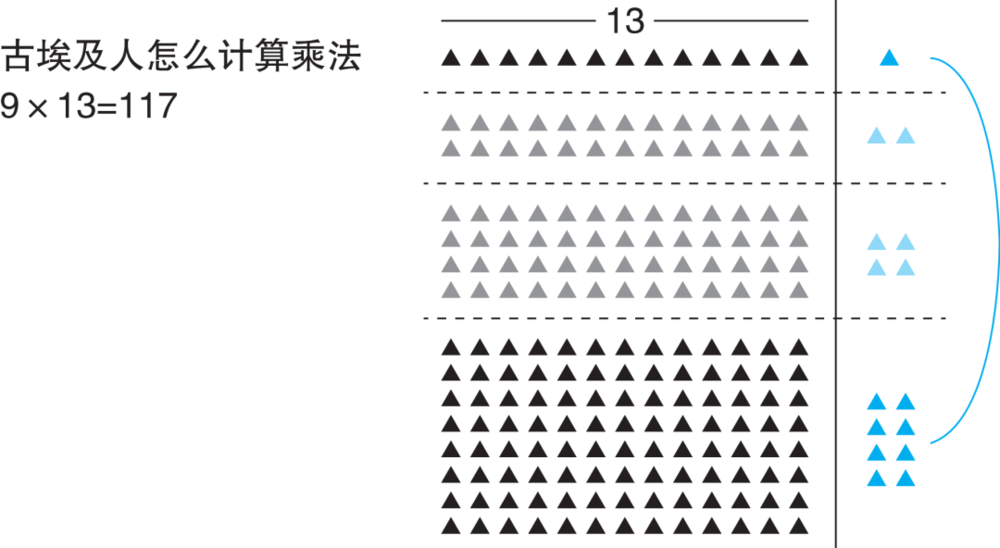
没错，117个。

天啊，这也太神奇了吧？就这么不断的左边翻倍，右边翻倍，最后把其中几行一加，就是正确答案？为什么啊？

其实不只是农夫乘法、古埃及乘法，这个世界上，还有印度乘法、划线乘法等等用来计算乘法的方式。

所有这些乘法，都是对的。因为他们都是准确而有用的。

但是如果说效率，九九乘法口诀的效率，是很少有别的方式能及的。

九九乘法口诀，是中国人在春秋战国时期发明的。秦始皇统一中国后，里耶秦简“九九乘法表”已成了当时的数学教材。13世纪，九九乘法口诀传入西方国家。

但是，中国的1~9，都是单音节。而英语里的one、two、three……nine，却有单有双。所以，很难有节律地背诵中国的九九乘法口诀。俄语就更复杂了。所以，伟大的九九乘法口诀，最终还是只在以中国为主的东亚地区广泛使用。

“九九乘法表”这一伟大发明，赋予了几乎所有中国人出色的基础计算能力。

如果你知道，你小时候背九九乘法口诀，居然这么有用时，你是不是背起来也会更加有兴趣呢？

所以说，数学，是有趣，而且有用的。

如果你觉得数学枯燥，而且脱离现实，除了考试之外毫无用处，那是非常可惜的。你错过了一门连接现象与本质之间的语言，你错过了理解商业世界最底层逻辑的终极方法。

这些终极方法，其实都是你学过的数学知识。

比如，前面提到的6种和商业高度相关的数学知识。

二、四则运算

什么是“商业世界的加减乘除”？

为了讲清楚这件事，我画了一张图。

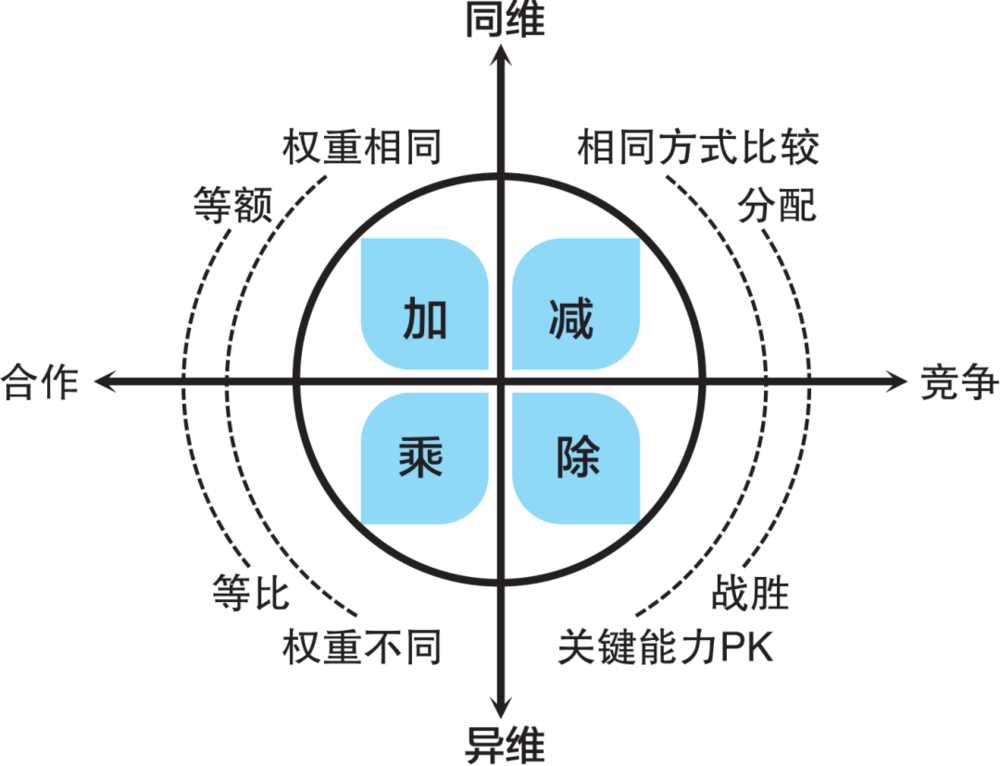
这张图的横轴，是竞争、合作。

商业世界的生命体，是企业。和生物世界的个人一样，企业也需要谋求个体的生存繁衍（竞争），和群体的共生繁荣（合作）。有时候，我们选择竞争，有时候我们选择合作。目的都是永续经营。

这比较容易理解。

这张图的纵轴，是同维，异维。

合作竞争，可能是在同一个维度上，也可能是在不同维度上。十个人都在种地，这是同维。大家的贡献是在同一个维度（种地）上的。但是，如果有人浇水，有人种地，有人运输，大家的贡献，就是在不同的维度上了。

为什么要理解竞争合作、同维异维？因为理解了这两件事情，你就能理解什么是“商业世界的加减乘除”了。

商业世界的加法，就是同维合作（左上角的象限）。

比如，你是怎么安排销售的工作的？安排10个销售，每个人都去独立发展客户，各自打粮食回家？如果是这样，你是在用“加法”管理公司。每个销售，都在用同样的方式，同样的权重，对公司的整体业绩做贡献。

但是有的公司不是这么做的。比如贝壳。贝壳管理公司的方式，是乘法。

商业世界的乘法，就是异维合作（左下角的象限）。

同样是房产中介，大部分公司是每个销售独立作战。但是，在贝壳的眼里，这种“散兵游勇”式的“加法管理”，是做不了大事的。为什么不试试乘法？

贝壳把房产中介的工作，分成了10个角色。没有任何一个人，可以独立完成销售工作，他们有各不相同的分工，然后协作，完成一单。他们对这一单的贡献维度不一样（10个维度），权重也不一样。

这就是异维合作，这就是商业世界的乘法。

商业世界里的最优秀的算法，基本都是乘法。

有意思。

那什么是商业世界的减法？

商业世界的减法，就是同维竞争（右上角的象限）。

市场份额总共100%，你拿了20%，我就少了20%。

公司定下来今年有2000万的市场预算。每个产品线报一下，你要多少？

产品线A，B，C，……，Z，都觉得自己挺重要，拼命抢，最后合并预算方案的总花费，将近2个亿。

你说减一减，每个人都愁眉苦脸，振振有词，说不能减，减了就做不下去了。老板很痛苦。

为什么会这样？因为每个产品线的竞争对手，是同维的另一条产品线。这就是：减法思维。

那怎么办呢？

试试用除法。

商业世界的除法，就是异维竞争（右下角的象限）。

每条产品线都想抢预算？

可以。但是，请不要和其他产品线抢。试着和你的“营收”抢。

预算（支出），和营收（收入），是不同维度的数字。不要让支出和支出竞争，要让支出和收入竞争。

怎么竞争？

算ROI。

所有产品线都可以来要预算。但是，这笔预算的年度ROI必须大于2，否则扣奖金。

你们回去自己先算算，然后再决定申请多少预算。

这时，每条产品线的竞争对手，已经不是其他产品线了，而是自己的营收能力。如果这时大家报上来的还是2个亿，你可能会笑着去借钱，都要给。因为这说明，团队们认为自己有能力打败营收能力这个强大的对手，而不是打败其他部门的同事。

这就是异维竞争。这就是除法。

除法的核心，是把两个关键经营数字，分别放在分子分母上，要求一个必须战胜另一个。

这就是商业世界的加减乘除。

每个公司，都有大量的数字。每个数字，都有它独特的价值。

而商业世界的加减乘除，就是从这些数字中，开采出矿藏的最基本手段。

三、笛卡尔坐标系

什么是“商业世界的笛卡尔坐标系”？

我举个例子。

比如，总有人问我一个问题：润总，我应该招什么样的员工，态度好的，还是能力强的？

这个问题很难回答。

因为这个问题的问法，就是典型的笛卡尔时代之前，把高维问题“降维思考”到一维视角之后，提出的问题。

我用一张图来表示，就是这样：

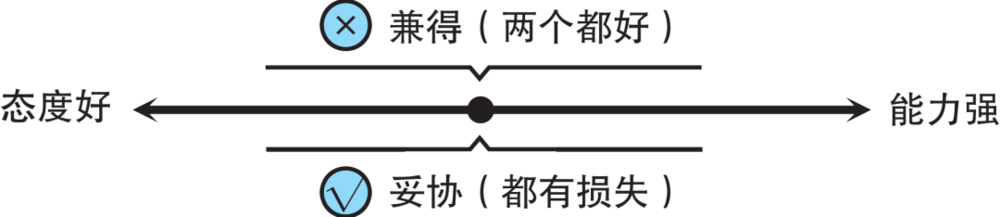
一维，就是一条线。态度好，是这条线的左端。能力强，是这条线的右端。要么左，要么右，不可兼得。这就是一维视角。

不对吧？这条线的中间，不就是“兼得”吗？

其实不是。中间不是“兼得”。中间是“妥协”。用能力差一点，换态度好一点。两个都有损失，但两个都“不太坏”。

但是，你想过没有，态度和能力，是一个维度上的事情吗？

态度本身就是一个维度。这个维度一端如果是“态度好”，那另一端只能是“态度差”。

而能力，是另外一个维度。这个维度的一端如果是“能力强”，那另一端只能是“能力弱”。

态度和能力，是不应该放在一条线上来做“二选一”的。它们是两个维度的事情。

笛卡尔如果听到这个问题，他可能会给你画一张二维直角坐标系，教你从二维视角来思考问题。

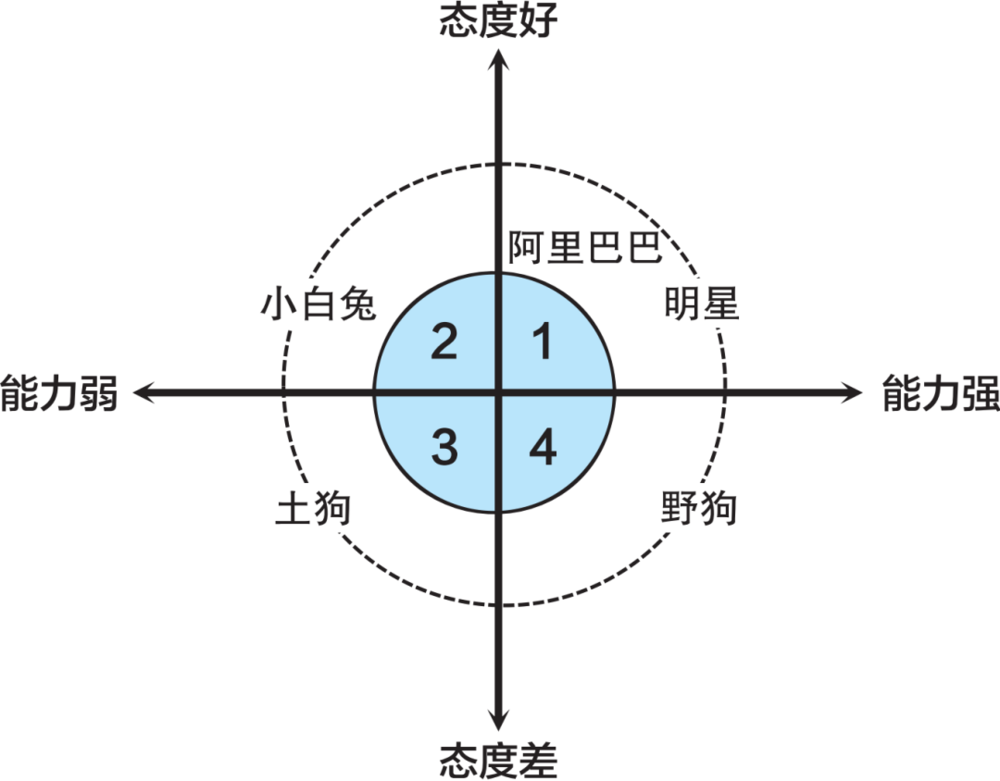
这个“二维直角坐标系”，用横轴（能力），和纵轴（态度），把可选的员工，分成了四个象限：

明星，能力强，态度也好；小白兔，能力弱，但态度好；土狗，能力弱，态度也差；野狗，能力强，但态度差。

当你如果能像笛卡尔一样“升维思考”，你就会发现，原来这个世界上不仅有能力强、态度差的“野狗”，或者态度好、能力弱的“小白兔”；还有两个都好的“明星”，以及两者都不行的“土狗”。

明星，小白兔，土狗，野狗。这就是阿里把员工分类的方法，是个典型的二维视角。

但是，我们再认真思考一下。

小白兔为什么要培养使用呢？小白兔值得培养吗？是想把小白兔的能力培养好，成为明星吗？如果这样，那为什么野狗不能也“培养使用”呢？把态度调整过来，也培养成明星呢？

这时，我们就需要继续升维思考。在态度、能力两个维度之上，引入第三个维度：可塑性。

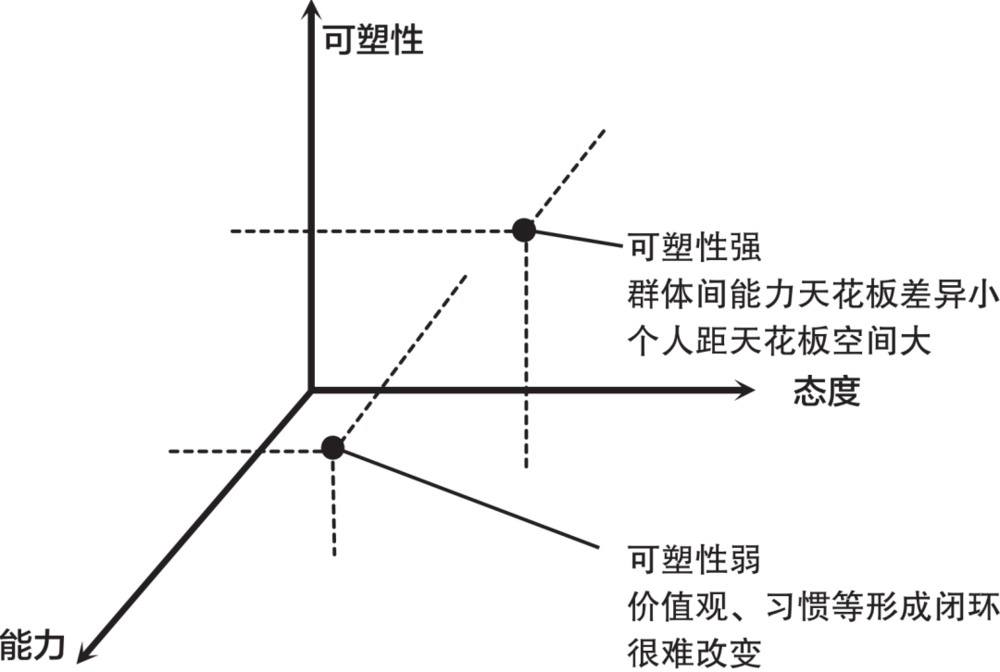
我们都想招到明星员工。但是明星员工毕竟是稀缺的。我们身边遇到最多的是土狗。其次是小白兔。然后是野狗。明星，很多都在大厂的关键岗位上，挖不动。

那怎么办？

把土狗、小白兔、野狗，培养成明星员工，可能才是可行之路。

那么，谁更容易培养？这就涉及“可塑性”这个维度了。

那么请问，是一个人的能力更可塑，还是一个人的态度更可塑呢？

当然是能力。

人与人之间，当下的“能力水平”，当然有差别。但是人与人之间“能力天花板”的差异不大。而且，大部分人离自己的天花板，还差很远。即便是明星。

所以，只要态度好，能力是“可塑”的。

但是态度就不一样了。

一个人的价值观，德行，态度，是过去几十年的人生经历塑造的。一旦形成闭环，非常难改变。除非是遇到一些重大的人生变故，大部分人会在自己的信仰、价值观、习惯里走不出来。态度的可塑性比较差。

所以，当我们用三维视角看问题，心中放的，就不仅是今天的明星员工，更是未来的明星员工。一套“员工培养体系”就会被建立起来，为公司的发展，不断“种植”明星员工，而不是“采集”。

这就是笛卡尔坐标系了不起的地方。

了不起在，他创建了一个重要的思维工具：维度。

一旦有了前后，左右，上下，三个维度后，我们混沌的思考，就可以被结构化地拆分为三个方向进行分别研究，然后再叠加起来深度思考。

这个过程，我称之为：升维思考。

四、指数和幂

什么是“商业世界的指数和幂”呢？

先来看一个算式：2³=8。这里面的3就是指数，8就是幂。而这个2，叫做底数。这种算法，叫做乘方。

我猜，你可能也看过这样两条算式：

1.01³⁶⁵≈37.8。

0.99³⁶⁵≈0.03。

这两条算式，看上去没有问题，也很励志。但问题是，它忽略了，有些东西的进步，是做不到每天1%的。比如说，劳动力水平。

你一天能组装200个手机。但不管你这一年内怎么提升自己，一年后都不可能一天组装756个手机。

体力劳动者做不到，脑力劳动者也做不到。

那谁能做到？

机器人。

所以，这和商业世界有关系吗？

有。我举个例子。比如选赛道。

我有个朋友，有次像发现新大陆一样激动地对我说：

“润总，我发现餐饮业到今天为止，都没有一家公司可以占据全国5%以上的市场份额。但互联网行业，一家公司可以占据70%。说明餐饮行业还有巨大的机会啊。餐饮业有4万亿的市场规模。如果我用互联网公司的方法进入餐饮业，也干到70%的市场份额，那不就是一家年收入将近3万亿的公司啊？比华为还大好几倍啊！”

他激动万分。

但，他用互联网的办法，就真的能做成一家年收入3万亿的公司吗？

你知道，今天中国最大的餐饮集团，是哪一家吗？

不是海底捞。是一家叫做“百胜中国”的公司。

如果你没有听说过百胜中国，你一定听说过它的品牌：肯德基、必胜客、小肥羊等。

百胜中国一年的营收大约为600亿元。

中国餐饮业总规模4万亿元，600亿大概占1.5%。

百胜中国，已经是极其受尊敬的餐饮集团了，你去研究它的管理方法，已经是令人叹为观止了。但是，依然只占中国餐饮市场的1.5%。在互联网行业，1.5%的市场份额，你都不好意思和人家打招呼。

为什么？

因为餐饮市场，天生是个趋向于“分散”的市场。

百胜中国，已经是一家上市公司，有“资本”的加持。百胜中国在互联网（会员、外卖）上也做了大量创新，所以也有“科技”的赋能。

但是，到最后的最后，肯德基的每一块炸鸡，都需要被具体的人炸出来，每一盒汉堡，都需要被具体的人包起来。虽然有资本和科技的加持，但是年收入600亿的百胜中国，更重要的依然是“劳动力”。

你猜百胜中国有多少员工？44万。

你想象一下，你管理40个员工的时候，是不是已经觉得很难了？管理400就更难了。管理4000，40000呢？

百胜中国管理了44万员工。如果要做到6000亿，占中国餐饮15%的份额，可能就需要440万员工，甚至更多。

科技公司华为，2021年营收6300多亿元。但是你猜华为有多少员工？13万。

科技公司用13万员工做到6000多亿元的收入。而餐饮业要做到同样的收入，可能要至少400多万员工。

到目前为止，地球上还没有一家公司，能管理400万员工。目前最大的是沃尔玛，大约230万。

也就是说，在餐饮业，一个以劳动力为主要生产要素的行业，几乎是不可能出现市场份额超过10%的巨头的。换句话说，在餐饮业，创业公司的收入，可能就不遵循幂律分布。餐饮业的创业公司的收入，可能会遵循正态分布。

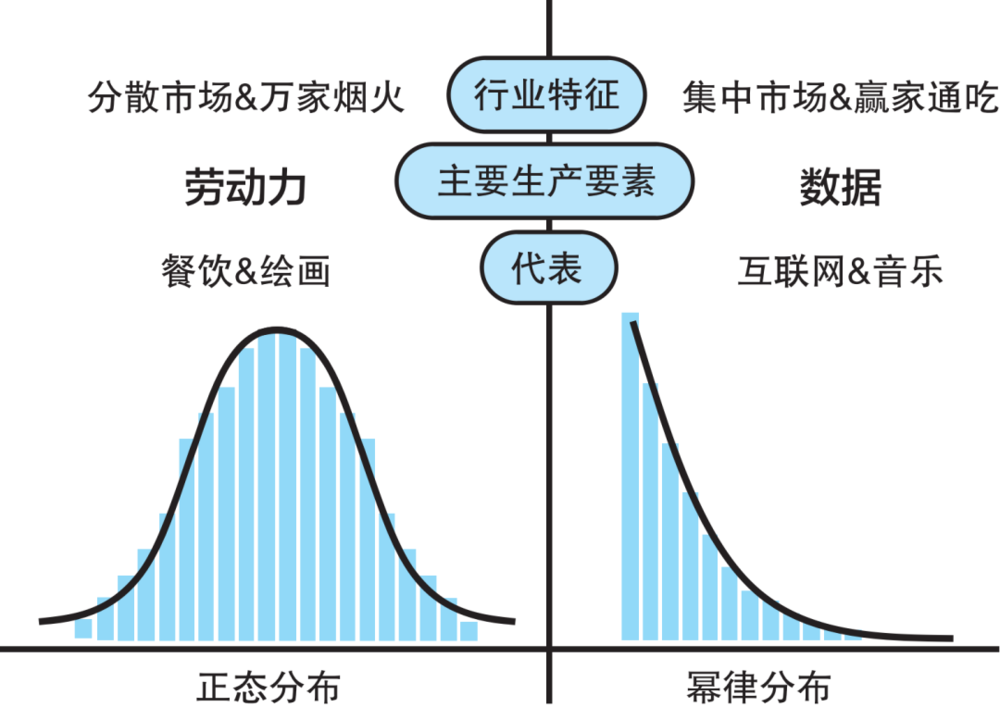
（正态分布&幂律分布）

所以，如果让你选，你要进入哪个行业，选择哪个赛道？餐饮业，还是互联网？

这是一个非常重要的战略选择。在数学规律的作用下，餐饮业，符合正态分布，而互联网，符合幂律分布。

理解了数学里的指数和幂之后，你才会明白，打打杀杀，都是小事。

选择在哪里打打杀杀，才是大事。

五、方差与标准差

什么是“商业世界的方差与标准差”？

方差和标准差，不是那么显而易见的概念。但是，它对你从更底层逻辑理解和指导经营管理，又特别重要。

所以，请允许我花一点时间，先从数学上稍微解释一下这两个概念。

什么是方差？

假设，X、Y两家公司，各有5名员工。两家公司的员工平均收入，都是72万。但是，每位员工的收入，并不一定是准确的72万。

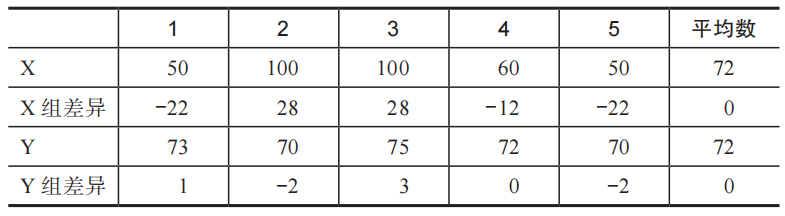
这时，你能一眼看出，X公司的员工收入，和平均收入的“差距”，要比Y公司大不少。

但是，这还是直观的感受。能不能从这组“个体差异性”数字，算出一个“群体差异性”指标呢？

能。这就是方差。

计算方差有两步。

先平方。平方的目的，是去掉正负号。

再均差。平均的目的，是得到差异性。

先平方，再均差，这就是我们用来衡量一组数据“差异性”的方法，叫“方差”。

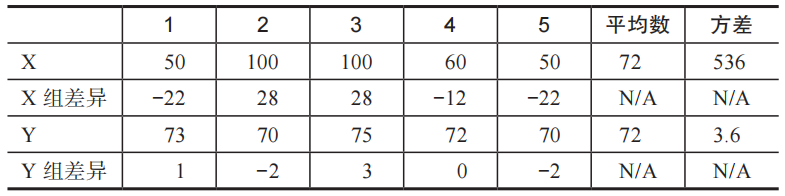
有了方差这个指标，现在就算在你面前摆1万家公司，你也能先给他们先打分，再排序，然后准确地说出任何两家公司，谁的收入更分散，谁的收入更集中了。

那什么是标准差？

标准差，就是方差的平方根。

X组数据的标准差，就是√536≈23.15。Y组数据的标准差，就是√3.6≈1.90。

回到工资的场景。

有了标准差，我们就可以说X公司的平均工资是72万，有23.15万左右的波动。Y公司的平均工资也是72万，有1.90万左右的波动。

所以，这和商业有什么关系？

有。质量的本质，就是标准差。

我举个例子。

假设，你是一家手机品牌商，新开发了一款前置摄像头手机，所以需要在表面玻璃上打孔。这个孔的直径，是7.2毫米。这款手机对你来说非常重要，所以你找了X、Y两家代工厂试样。

很快，两家工厂各自给你交回来5块打好孔的样品，并告诉你，孔直径正好是平均7.2毫米。可是，你测量了每一块玻璃，发现数据居然各不相同。

X工厂就是个坑啊。5毫米，10毫米，10毫米，6毫米，5毫米，没有一个在7.2毫米附近。你一算，发现标准差是2.32毫米。

你的手机，其实经过一定的容错设计。7.2毫米±0.3毫米其实都可安装。但是X工厂的产品标准差实在是太大，2.32毫米，以至于没有一个样品在容错范围内，最后没有一款产品可以使用。

而Y工厂，最小的孔是7毫米，最大的孔是7.5毫米，都在7.2毫米±0.3毫米的容错范围内。一看，果然标准差很小，只有0.19毫米。所以，Y工厂的打孔玻璃，都可以用。

所以，你会和哪一家工厂合作？

当然是Y工厂。因为X工厂标准差太高，以至于最后的良品率是0；而Y工厂的标准差控制得很好，良品率是100%。

同样是生产打孔玻璃，我们说Y工厂生产的打孔玻璃：质量更高。

所以，什么样的产品，质量更高？

标准差更小的产品，质量更高。因为标准差越小，性能越稳定；性能越稳定，质量越高。

这就是方差和标准差的意义。

其实差异性，我们很多时候是能感受到的。

那为什么还一定要用数学来量化呢？

因为只有量化了的差异性，才是可以比较的差异性，才是可以改进的差异性，才是可以作为健康指标的差异性。

六、概率与统计

什么是“商业世界的概率与统计”？

概率，是用于个体的概念，用来“衡量”一件事情，将要发生的“可能”的大小。对于“好的事情”，衡量“运气”的好坏；对于“坏的事情”，衡量“风险”的大小。

统计，是用于群体的概念，用来“计量”一群样本，满足条件的“比率”的大小。对于“多的事情”，计量“普遍”的幅度；对于“少的事情”，计量“稀缺”的程度。

关于概率与统计还有很多相关的数学概念，我仅举一例：大数定律。

什么是大数定律？

我给你讲个故事吧。

在做咨询之前，我在科技行业工作了很多年，所以很幸运，共事，或者结识了大量科技行业的同事、朋友、老师。

开始做咨询之后，他们其中有些人离开原来的公司创业，也会来找我聊聊。我会给些自己的建议。甚至，会参与一些投资。

没想到，我的第一个投资项目，就获得了不小的收益。

有一次，我和五源资本（原来晨兴资本）创始合伙人刘芹聊起这件事。

五源资本是中国最著名的VC之一。他们投过的项目，像小米、快手等等，都获得了相当好的回报。刘芹给我分享了他的投资经历。

他说，他的投资生涯，分为了三个非常明显的阶段。

第一个阶段，是看什么项目都觉得是好项目。

哇，这个创始人太厉害了，这个项目太好了。每个人身上都有闪闪发光的点，每个项目都有独到之处。当然，有些项目成功了。但是没想到的是，更多项目失败了。

第二个阶段，他看什么项目都觉得有问题。

这个团队有问题，这个产品有问题，这个股权结构有问题，这个市场定位有问题。如果你想找问题，你一定能找出问题。面对数不清的问题，刘芹说他总是不敢出手。但是，不出手虽然没有风险，但也因此没有收益。

第三个阶段，他开始逐渐形成了一套自己的投资原则。符合这个原则的，再有问题，都是可以投资的；不符合这个原则的，再闪亮的创业者都不碰。这套原则，让他避开了很多坑。当然，也漏掉了不少好项目。但如果把所有用这套原则投过的项目收益拉平了来看，是成功的。

我听了之后，豁然开朗。

用数学的语言表述，刘芹的“投资原则”，就是一个自己打磨出来的、极其宝贵的“数学期望”公式。

每见到一个创业者，他就把创业者的情况代入进去算一下。如果算出来的数学期望为正，就投。数学期望为负，就不投。

那么，会不会数学期望为正的创业者，最后创业失败；而数学期望为负的创业者，反而成功了呢？

当然有。

但是，如果你投10个，100个，甚至1000个项目后，就会发现，这些“个体的不确定”会被逐渐磨平，慢慢浮现出“群体的确定性”。最后1000个项目的平均收益，无限接近“数学期望”。

这就是“大数定律”。

用最简单的例子来表述就是，如果掷硬币得到正面的概率是50%，那么掷的次数越多，就会有越接近一半的硬币是正面。

因为大数定律，个体的不确定性，被转化为了群体的确定性。

所以，到底什么是投资？

投资，是个数学游戏。

一个专业投资人赚的，其实从来都不是1个项目的巨额收益。那有“个体不确定性”。

投资人赚的，是10000个项目的平均收益。那有“群体的确定”。

而一个“顶尖的”专业投资人之所以顶尖，是因为他独有的投资原则的“数学期望”比别人高，同时他对“大数定律”的信仰比别人强。

我问刘芹，那你用了多少年，才走到第三阶段，找到自己的“投资原则”的呢？

刘芹说，15年。

听完后我决定，除非特殊情况，我再也不直接投项目了。我投的这个项目，纯粹是上天赏饭吃，靠运气。

一身冷汗。

这就是概率与统计。

因为这个世界，从来都不是确定的。

七、博弈论

什么是“商业世界的博弈论”？

你可能在经济学的书里看过博弈论，在社会学的课里听过博弈论。是的，博弈论的应用很广。但是谈博弈论，首先是个数学问题。发明博弈论，以及对博弈论起到巨大贡献的冯·诺依曼、约翰·纳什，都是数学家。

关于博弈论的重要概念也有很多，我仅举一例：收益矩阵。

收益矩阵，又叫支付矩阵，又叫报酬矩阵，又叫赢得矩阵，又叫得益矩阵。

很多名字，但都有“矩阵”这两个字。因为一旦决策者从单人，变为至少双人，决策的结果，就从一维的“得失”，变为二维的“利害关系”问题了。

石头剪刀布，就是最典型的例子。

A和B石头剪刀布。对A来说，出剪刀，石头，还是布的“得失”最大呢？显然，这要取决于B出什么。B的选择，和A的选择，共同决定了彼此的“利害关系”。

我用一张表来表示。

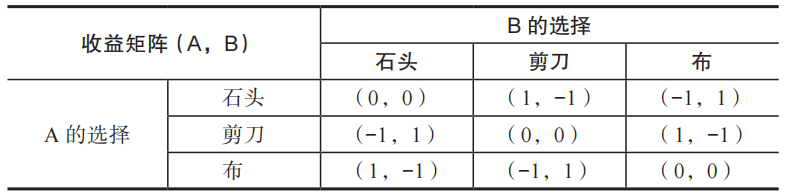
这张表，就是收益矩阵。

A和B都关心自己的“得失”，但是他们的“得失”交织在一起，构成了这张“利害关系”图。

当A出石头时，如果B出剪刀，则收益为（1，-1）。

这意味着A加1分，B减1分。

但是如果B预判了A的石头，出了“布”，那收益就变为了（-1，1），情况完全逆转，变为了A减1分，B加1分。

但是如果A预判了B的预判，知道B预判自己出石头，所以出布，于是就出了剪刀（有点拗口啊），情况就再次逆转，收益变为（1，-1），A加1分，B减1分。

然后，B再继续预判A对B预判的预判……

他们拳不动，心在动。两人在心里不断博弈，他们各自的得失，就在这张“收益矩阵”里不断游走。6轮之后，又回到原点。

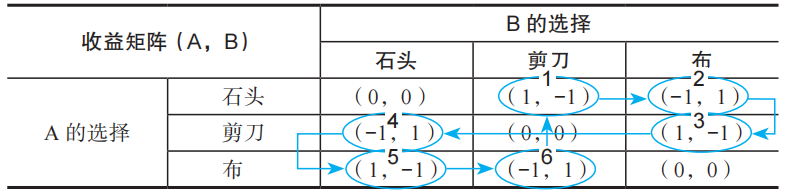
这就是收益矩阵。

每个用“语文”来描述的游戏规则（Game Rule），翻译成“数学”，就是一张收益矩阵的表。决策双方，在这个收益矩阵里，研究如何扩大自己的赢面。最好稳赢。

那么，在石头剪刀布的游戏规则下，这张收益矩阵表里，有谁可以“稳赢”吗？

没有。

一个“稳赢”的游戏，是一个没有生命力的游戏。围棋、象棋、国际象棋、五子棋，这些流传了几百上千年的游戏，都没有稳赢的策略。

因为如果有人能稳赢，那必然会输掉的一方就不参与了。所以这个游戏，就流传不下来。

那研究博弈论还有什么意义？

博弈论的很多重要概念，比如收益矩阵、占优策略、纳什均衡，都能帮助你更好地理解商业世界的，诸如投广、进货等问题。

或者说，在某些特定规则下，是能够做到“稳赢”的。

因为博弈论，能帮你研究如何在复数主体下，做战略决策。

最后的话

这就是我今天想和你分享的底层逻辑，和6个相关的数学知识。

希望对你有所启发。

在《底层逻辑2》中，还有更多其他的知识，帮助你建立底层逻辑，解决商业世界的各种问题。

当然，数学这种底层逻辑，并不局限于商业世界。

数学，可以帮助我们看清世界的真相。

不平均的真相，不公平的真相，人性的真相。

但是，借用罗曼·罗兰的一句话：真正的英雄主义，是看清生活的真相后，依然热爱生活。

因为在这样的真相之下，我们依然可以创造美好。

是的。看清真相，创造美好。

最后的最后，我也斗胆邀请你，和我一起通过底层逻辑，看清世界的底牌。

本文来自微信公众号：刘润 （ID：runliu-pub），观点：刘润，主笔：二蔓，责编：黄静