

扫码打开虎嗅APP
题图来自:IC photo,本文来自微信公众号:原理(ID:principia1687),撰文:Christian Yates(巴斯大学数学生物学高级讲师)
自从人类出现以来,疾病一直如影相随,折磨着人类。5000多年前,疟疾和肺结核曾在古埃及肆虐。从公元541到542年,被称为查士丁尼瘟疫(Plague of Justinian)的全球大流行疫情估计造成了全球2亿人口中15%-25%的死亡。在西班牙征服墨西哥后,当地本土人口从1519年的3000万,50年后下降到仅剩300万。如今,我们正在努力控制COVID-19的扩散,而它有可能成为人类历史上最致命的大流行之一。
然而,一个鲜为人知却极为成功的科学领域,正致力于揭开传染病的神秘面纱。数学流行病学在抗击COVID-19这样的大规模传染病中,起到了关键作用。
通过基本的数学模型,研究人员可以预测疾病的进程,了解干预措施对疾病传播的影响。有了更复杂的模型,我们就有可能回答一些更关键的问题,比如应当如何有效分配有限的资源,了解关闭酒吧和禁止聚会等这类公共卫生干预措施所带来的效果。
数学模型所提供的信息对确保当局尽可能地阻止死亡来说至关重要。随着COVID-19大流行逐渐升级,下面我们来看看,专家如何借助模型,努力走在病毒前面。
一、S-I-R模型
一个最简单的疾病传播的数学模型之一会根据疾病的情况,将人口分成三个基本类别。没有患过这种疾病的人被称为易感者(Susceptible)。每个人都被认为天生易受到感染,且能够被感染。那些感染了这种疾病,并能把它传染给易感者的,就是感染者(Infective)。第三类被委婉地称为移出者(Removed)。这些人包括患了这种病后来康复,且现在已经免疫的人,也包括已经死亡的人。这些“移出”的个体不再参与疾病的传播。
这被称为S-I-R模型。从拉丁美洲的登革热,到荷兰的猪瘟,还有比利时的诺如病毒,S-I-R模型可以为预防疾病传播提供关键信息。
这个模型说明了对感染者进行社会隔离的重要性。如果感染者待在家里,直到完全康复,他们可以有效地从感染者这一类别,直接转移到不会感染病毒的移出者类别。这个简单的行为能够降低疾病传染给易感者的机会,从而缩小疫情的规模。
一次暴发是继续扩散还是消失,很大程度上取决于这次暴发中的一个关键数字——基本再生数。
在2019年12月COVID-19暴发之初,全球人口都是这种疾病的完全易感人群。新发疾病的一位携带者传染给以前未暴露的个体的平均人数,被称为基本再生数,通常用R₀表示。
如果一种疾病的R₀小于1,也就是每位感染者平均将该疾病传染给少于一个其他个体时,那么该疾病将迅速消失,疫情无法继续蔓延。而如果R₀大于1,那么疫情将指数增长。
二、指数暴发
早期对COVID-19的基本再生数的估计在1.5到4之间,在12月和1月间的数值应该不小于2。在基本再生数等于2的情况下,第一个感染疾病的患者会将疾病传播给另外两个人,而每个受到感染的人平均又会将疾病再传播给另外两个人,以此类推。
这种指数增长是感染的初期特征。如果放任这种传播继续下去,经过10代的传播链,超过1000人会被感染。再往前“走十步”,数字就会超过百万。
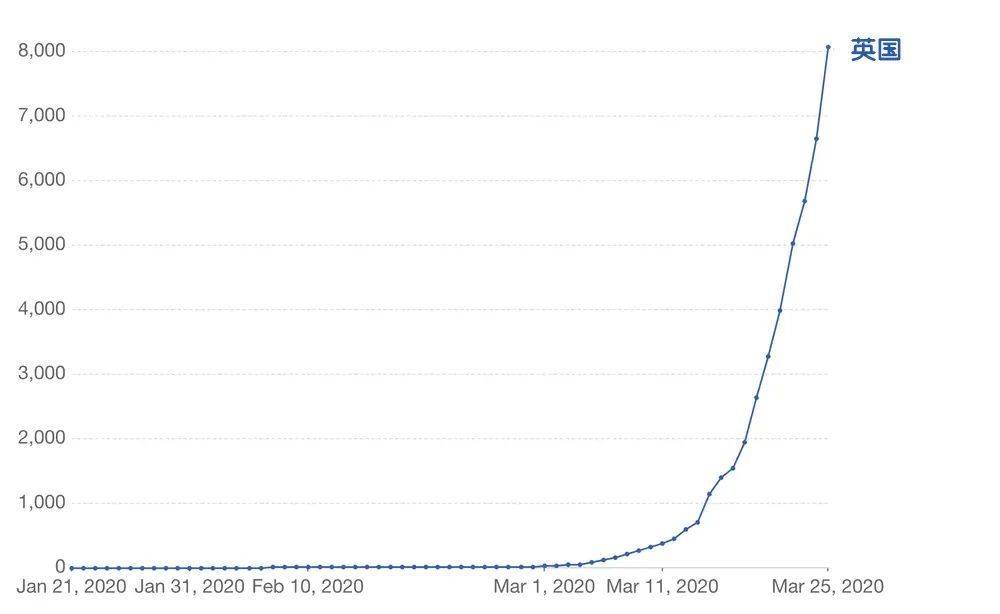
○ 英国新的COVID-19确诊病例总数,在近期呈指数增长。(确诊病例人数低于总患病人数。这主要由于是检测能力的限制。)| 图片来源:European CDC/OurWorldInData.org/coronavirus
实际上,由基本再生数预测出的指数增长,很少能维持几代以上。由于感染者和易感者接触的频率下降,疫情的发展最终会达到一个高峰,然后逐渐下降。
即使疫情正式结束,没有留下感染者,一些易感者仍然存在。S-I-R模型可以估计流行病的最终规模,估算出如果不采取补救措施,在疫情结束时受感染的人数。在对COVID-19的估计中,在数量最少的估计情况下,再生数为1.5,这意味着58%的人口将受到感染。而在更高的估计中,R₀是4,S-I-R模型预测,如果不采取行动,只有2%的人不会受到感染。
三、一个关键的数字
基本再生数有助于了解几乎所有疾病的暴发,因为它把疾病传播的几乎所有细节都归纳为一个数字。从疾病在体内发展的方式,到传播的模式,甚至是疾病传播的社会结构,它捕捉到疫情所有的关键特征,让我们能做出相应的反应。
R₀通常可以被分为三个部分:人口规模、易感者被感染的速率(通常称为感染力),以及疾病康复或死亡速率。增加前两个因素,R₀会随之增加,而增加治愈率,则会降低R₀。人口越多,疾病在个体间的传播越快,疫情的规模可能就越大。个体康复得越快,他们能将疾病传染给他人的时间就越短,这样疫情的控制就相对更简单。
还有一个数字是有效再生数。这是在疫情发展到某个特定时间,由感染者引起的继发感染的平均数。通过干预,如果有效再生数能降到1以下,那么疾病就会消失。
四、病死率
尽管R₀对控制疾病至关重要,但它并不能告诉我们,对被感染的个体来说这种疾病有多严重。最终死于疾病的感染者比例,叫作病死率。
极具传染性的疾病,比如麻疹,其R₀在12到18之间,而埃博拉的R₀大约在1.5左右,比麻疹小得多。但50-70%的埃博拉病毒感染者会死亡,相比之下,麻疹的病死率较低。因此,人们通常认为,麻疹没有埃博拉严重。早期估计表明,COVID-19的病死率在0.25%到3.5%。
但是一定要记住,病死率并不是固定不变的,它取决于社会和个体对该疾病的反应,以及它所感染的人群的人口统计特征。例如,COVID-19的病死率似乎随着患者年龄的增长而显著变化,老年人受到的影响最严重。

○ 截至2020年2月11日,COVID-19在中国不同年龄群体的病死率统计。相比于整体人口,老年人的病死率最高。| 图片来源:European CDC/OurWorldInData.org/coronavirus
或许会让人惊讶的一点是,病死率高的疾病往往传染性较低。如果一种疾病太快杀死了太多的受害者,那么它就减少了自身被传染出去的机会。又能导致大多数感染者死亡,又能有效传播的疾病非常罕见,它们通常出现在灾难片里。
尽管在疫情暴发期间,高病死率会显著增加人们的担忧,但高R₀而病死率较低的疾病,或许会因感染人数更多,而最终导致更多人死亡。(想想COVID-19和埃博拉的差异。)
五、控制疫情
接种疫苗是减少疾病传播最有效的手段之一。让易感者绕过感染,将他们直接转移到移出者,可以有效地缩小易感人群的规模。
但疫苗通常是一种预防措施,在最初能用来降低暴发的可能性。一旦像目前COVID-19大流行这样的疫情已经全面暴发,在有效的时间框架内开发和测试疫苗往往不切实际。
检疫和隔离能有效地降低传播率,从而降低有效再生数。隔离感染的患者能降低传播率,而检疫隔离健康的个体则可以缩小有效的易感人群。
这两种手段都有助于降低有效再生数,这就是为什么保持社交距离和自我隔离是应对COVID-19非常重要的策略。
六、群体免疫
英国政府在疫情初期似乎提到的一个想法是群体免疫,也就是大量免疫的个体可以减缓甚至阻止疾病的传播。这种群体效应并不要求每个人都对疾病有免疫力,就能保护整体人口。通过将有效再生数量降低到1以下(确保感染者接触尽可能少的易感者),传播链可能被打破,疾病的扩散也会停止。最关键的是,群体免疫意味着,免疫力低下的人、老年人、孕妇和其他高危人群可以受益于其他人群的免疫力所提供的保护。
为了保护其他人,而需要自身获得免疫的人口比例,因疾病传染性的不同而有所差异。基本再生数R₀决定了这一比例要有多大。基本再生数越高,所需的免疫群体的比例就越高。例如,对于一种基本再生数为4的疾病,S-I-R模型预测,四分之三的人口必须获得免疫。如果R₀低至1.5,可能约三分之一的人口需要获得免疫,来保护剩下三分之二的人。
如果有疫苗,就可以通过接种足够高比例的人群,来实现群体免疫。(即便如此,我们通过接种疫苗才完全消灭过一种疾病——天花。)
当没有疫苗时,人们获得免疫的唯一途径就是感染这种疾病并康复。根据COVID-19的病死率,这将意味着数千人死亡。不出所料,英国政府收回了他们提出的政策。
七、下一代模型
实际上,简单的S-I-R模型还不够复杂,不能捕捉许多传染病暴发的最细微之处。但是对于那些不会让患者获得疾病免疫的疾病,对S-I-R模型的简单修改也会有所帮助。
淋病是性传播疾病的典型例子之一,它根本不存在移出者。患者一旦从淋病中康复,就可能再次感染。由于没有人死于淋病的症状,也从来没有人因此被从人群中“移出”过。这类模型通常被称为S-I-S模型,它们模拟个体“从易感到感染再回到易感”的发展模式。由于易感人群从未耗尽,但会随着人们的康复而更新,S-I-S模型预测疾病可能会自维持或“流行”。
在COVID-19暴发开始时,科学家最担心的问题之一包括,一次感染是否足以给患者提供免疫。这种新型病毒会在人群中无限期地传播下去吗?尽管已经有报告称,有人二次感染了这种病毒,但同样存在有力证据表明,康复的COVID-19患者能够获得免疫。
有关新型冠状病毒的另一个问题是,在疾病感染初期,通常存在一段无症状时期。在这段时间里,感染者携带的病毒会“隐藏”,这些感染者没有表现出症状,但有能力感染其他人。这意味着我们需要在模型中添加另一类人。这些人一旦被感染,就能够在没有表现出任何症状的情况下传播疾病,他们被称为携带者(Carrier)。这将S-I-R模型演变为S-C-I-R模型。携带者类别对于以HIV/AIDS等为代表的无明显症状时的传染期长的疾病至关重要。
目前用于为政府政策提供信息的最先进模型更为复杂。但不幸的是,即使是最详细和最贴近现实的数学模型,也无法预测当前的大流行究竟何时能得到控制。
但可以肯定的是,当我们最终控制疫情时,数学家和他们的模型将在这个发展过程中发挥重要作用。
本文来自微信公众号:原理(ID:principia1687),撰文:Christian Yates(巴斯大学数学生物学高级讲师)。原文标题“How to model a pandemic”,于2020年3月25日发表于The Conversation,原文链接:https://theconversation.com/how-to-model-a-pandemic-134187。文章通过CC协议翻译,中文仅供参考,一切以原文内容为准。
