月球昼夜温差高达300°C，月球车车轮应该如何设计？

本文来自微信公众号：中国工程院院刊（ID：CAE-Engineering），选自中国工程院院刊《Engineering》2020年第8期，作者：杨璐，蔡博文，张荣辉，李克宁，张子贤，雷洁浩，陈百超，王荣本，原标题：《月球车车轮应如何设计以适应月表行驶？》，题图来自：视觉中国

在过去或未来的探月计划中，月球车一直是月表探测的关键所在。月表温度白天可达150 °C，而夜间又低至−180 °C，巨大的温差使地球上成熟的车轮技术很难在月球表面应用。受限于月球车有限的空间，再加上月表地形复杂，大大增加了车轮系统设计和优化工作的难度。那么，月球车车轮需具备哪些特征？月球车车轮应如何设计以适应月表行驶？

中国工程院院刊《Engineering》刊发《月球车叶片伸缩式步行轮的力学分析和性能优化》一文，针对我国自主设计的月球车机械结构，提出了一种新型叶片伸缩式步行轮，并建立了一个原理型样机对其性能进行优化。为应对月表复杂路况，文章指出，以功耗最小化为目标，在保证障碍通过性的前提下，分析月球车车轮运动过程中受力情况以实现对车轮的性能优化，并基于数字仿真和综合实验方法，验证了新型车轮系统在实际实验中可以达到按需伸缩叶片和节约能耗的效果。总之，这种全新的步行移动系统设计方案可以为解决月球车在月表行驶时面临的通过性以及能耗问题提供有用参考。

一、概论

月球探测相关计划一直广受世界各国关注。月球着陆更是探测计划中要执行的最重要的任务之一。过去有中国的嫦娥3号和美国的阿波罗13号，现在，世界各国又将开展新一轮的探月计划（中国2025载人登月计划；美国重启阿波罗计划）。无论在过去或未来的探月计划中，月球车都是月表探测的关键所在，其被要求能够运行在路况和环境都十分复杂的月表上。其中，月表温度在白天可达150°C，而在夜间又低至−180°C，如此巨大的温差使地球上成熟的车轮技术很难在月球表面应用。

由此，月球车车轮应具有以下特征：

（1）使月球车具有较高的牵引和承载能力；

（2）月球车轮能够通过复杂地形和障碍。

在月表，岩石、陨石坑和斜坡呈不规则分布。且月壤的粒径和松软程度差异很大。各国为此设计了多种车轮结构。其中，三个已经成功降落在月球：前苏联的Lunokhod使用的弹性车轮以及美国阿波罗探月飞行器（LRV）（图1）和玉兔号均使用了相似结构的弹性筛网轮（图2）。同时还有其他有关车轮结构的研究成果，如哈尔滨工业大学开发的圆锥形车轮和北京航空航天大学设计的抓钩智能可变径车轮（图3）。它们都对月表具有很强的适应性。

图1 阿波罗LRV

图2 玉兔号

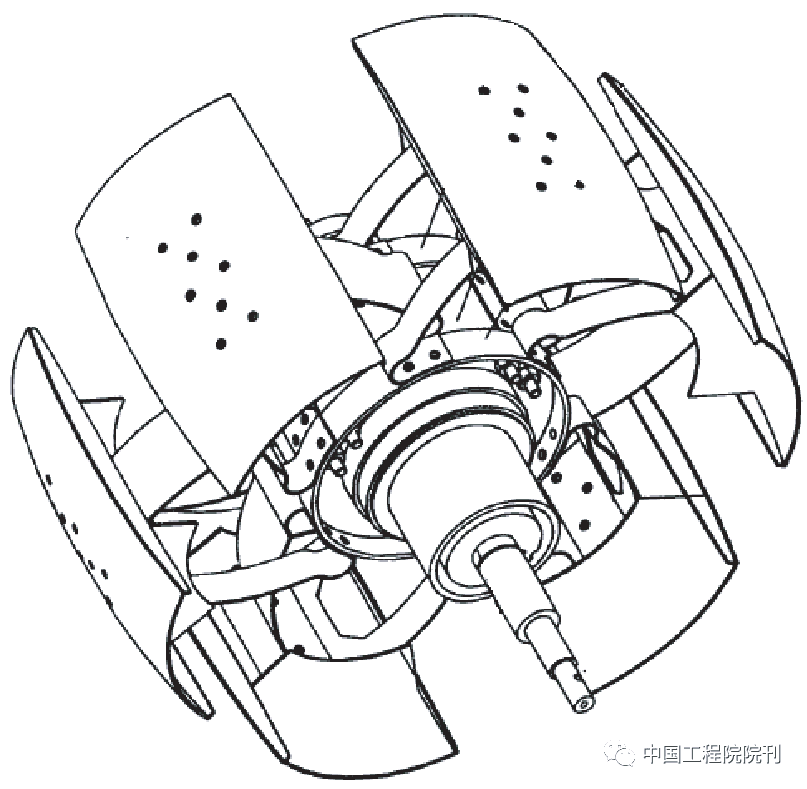
图3 智能可变径车轮

在现有的车轮设计中，弹性筛网轮在负载很大时容易变形，圆柱、圆锥形车轮在撞击时易断裂，智能变径车轮结构复杂、可靠性低、容易损坏。而且，尽管这些车轮具有较强的越障能力，但它们的功耗控制较差，无法满足未来探月的复杂要求。因此，十分有必要设计出一款性能均衡的新型车轮。

为满足复杂的月面探测要求，本文提出了一种新型的车轮系统。该系统基于吉林大学智能汽车研究组设计的叶片式伸缩式步行轮（图4）。其对月球软土具有高适应性，本文选择该模型作为原型。新型车轮系统的主要优点是可以根据路面状况（如松软度和坡度）和障碍物（如尺寸）自动调整叶片伸出长度。

图4 叶片伸缩步行轮结构

对于叶片伸缩式步行轮来说，车轮叶片越长意味着更好的车轮通过性。同时，车轮能量消耗会随着车轮阻力增大而增大。因此，理想的伸展条件是叶片能够根据地形需要伸出，从而节约能量消耗。

本文基于以下目标设计新型车轮系统，以便月球车可以根据需要控制能耗通过复杂路况：

（1）提出了一种新的叶片伸缩式步行轮，用于带有正反四边形悬架的月球车；

（2）对叶片伸缩式步行轮的设计参数进行优化；

（3）在模拟月表土壤环境中对实验模型进行评估；

（4）设计并测试了新的月球车原型机。

本文的其余部分安排如下：第二部分对新型车轮系统进行力学分析；第三部分对叶片伸缩式步行轮的参数进行优化；第四部分模拟月球土壤环境对原型机进行评估；第五部分对本文进行总结，并提出了一些可行的未来工作。

二、叶片伸缩式步行轮的力学分析

在对叶片伸缩式步行轮进行优化之前，本文首先根据月球表面的真实情况对新型车轮系统进行力学分析，分析后由所得结果设定车轮结构尺寸。在此，新型车轮系统将基于吉林大学智能车辆研究组提出的CJ-1（正反四边形悬架月球车）模型进行设计。

在图5中，L₁ = 453.3 mm, L₂ = 191.65 mm, L₃ = 212.1 mm, L₄ = 218.72 mm, L₅ = 145.05 mm, L₆ = 431.86 mm, L₇ = 142.24 mm, L₈ = 342.6 mm, L₉ = 141.4 mm, L₁₀ = 354.2 mm, L₁₁ = 400.1 mm, L₁₂ = 135 mm, γ₁= 38.31°,  γ₂= 41.76°, γ₃ = 53.62°, γ₄ = 68.29°, γ₅ = 17.36°,  γ₆= 44.9°, γ₇ = 42.3°,  a₁= 938.3 mm,  a₂= 359.5 mm,  a₃= 307.8 mm, a₄ = 179.1 mm。

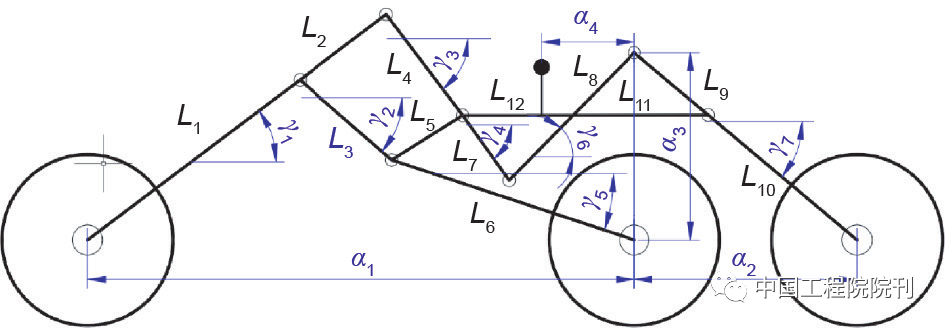
图5 实验模型各杆件尺寸

根据CJ-1模型结构尺寸，车轮半径R定为150 mm，车轮质量定为3.5 kg，模型整体质量定为120 kg。在月球重力场下，W₁ = W₂ = W₃ = 5.7 N，G = 80.85 N。

斜坡是月表常见的障碍。对于月球车必须通过的多种道路条件，上坡是反映车轮受力状态最直观、有效的状况。当月球车爬升时，车轮受力可达到最大参数，所以车轮的牵引力在爬升过程中可以得到有效检验。在本文中，车轮受力分析以θ_s的斜率进行（图6）。

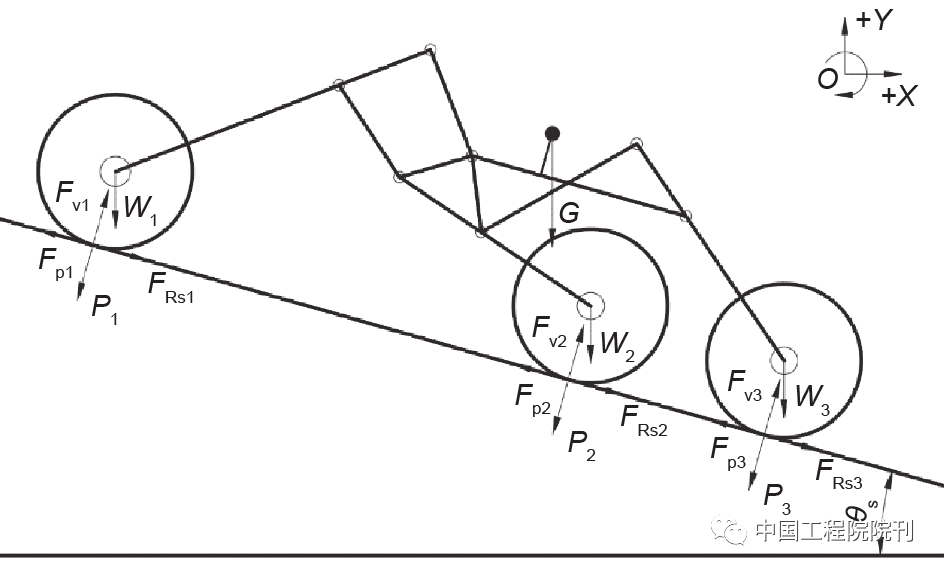
图6 在坡度θ_s下的系统受力分析

道路的支持力F_v和车轮对地压力P是相互作用力。地面摩擦力F_p和倾斜阻力F_Rs也是相互作用力。因此，如表1所示，可知月球车的坡度阻力和道路压力。

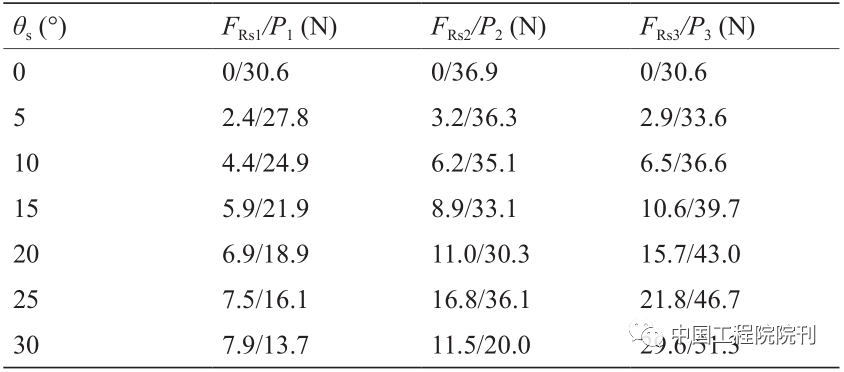
表1 不同坡度θs条件下坡度阻力FRs和压力P的关系

三、叶片伸缩步行轮的优化参数确定

新型车轮系统设计的难点在于月表的复杂地面情况。在月球表面，需要考虑不规则的石头、火山以及颗粒度和柔软度不同的月球土壤。由于常见轮胎的牵引能力不足以将月球车拉出松软的月球土壤，因此传统车轮对月表环境适应性极差。为了弥补常见轮胎的不足，本文提出了一种自动伸缩叶片结构。首先，本文对车轮和土壤之间的受力进行分析。

（一）车轮和土壤之间的受力分析

车轮受力可分为土壤推力（ST）和土壤阻力（SR）。如果ST大于SR，则车轮将向前移动。否则，车轮将空转或静止。在这里，SR包括四种阻力：土壤压实阻力（SCR）、土壤推土阻力（SBR）、土壤坡度阻力（SSR）和土壤叶片阻力（SVR）。下面对土壤推力和四种土壤阻力进行详细解释。

1. 压实阻力

在车轮转动过程中，车轮对月壤垂直向下挤压。这时，土壤产生防止自身形变的压实阻力。压实阻力F_Rc 可以表示为：

式中，z₀是轮缘的下沉深度，z₀=

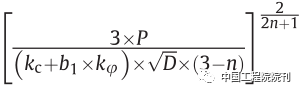
k_c是土壤的内聚模量；k_φ是土壤的摩擦模量；n是土壤变形指数；b₁是轮缘的宽度；D是轮缘的直径；P是车轮对土壤的压力。

2. 推土阻力

除了垂直方向的阻力以外，轮子前进过程中的推力也会引起土壤变形。这就是推土阻力（SBR）。车轮前的土壤呈波浪形形变，所以推土阻力F_Rb可以通过式（2）表示：

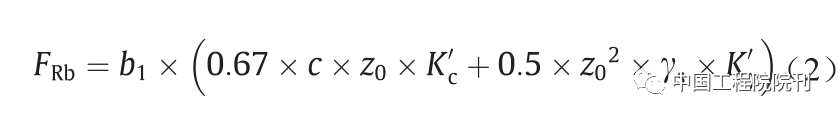
式中，

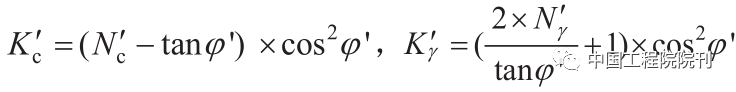
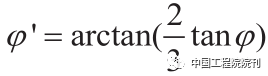
γ_s是堆积密度；c 是内聚力；φ 是内摩擦角；N_c^′和N_γ^′是太沙基承载系数，其值在表2中提供。

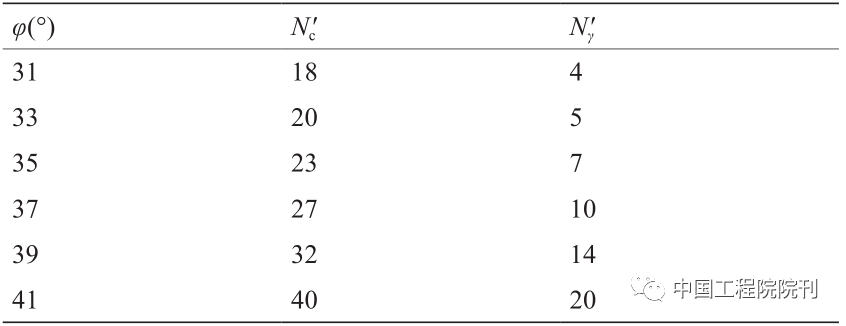
表2 太沙基承载系数 

3. 坡度阻力

当月球车爬坡时，在斜坡方向上的重力会产生坡度阻力，可以表示为：

式中，W_i 是第i 个轮子的重量；θ_s是倾斜角。

4. 叶片阻力

在滚动过程中，叶片在垂直方向上压缩土壤，而土壤会阻止垂直挤压力形成叶片压实阻力，这就是所谓的叶片阻力。叶片阻力F_Rv可以表示为：

式中，N是叶片数量；b是叶片厚度；b₂是叶片宽度；S是车轮滑转率；h_b是叶片插入深度。根据对月球土壤的抽样分析，土壤变形指数n通常等于1，因此车轮S的滑转率为n–1 = 0。因此，叶片阻力不受滑转率的影响。

5. 土壤推力

轮缘受到的最大土壤推力F_w可以表示为：

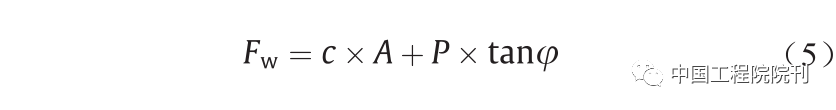
式中，A是轮缘和土壤之间的接触面积：

叶片受到的最大土壤推力F_s可以表示为：

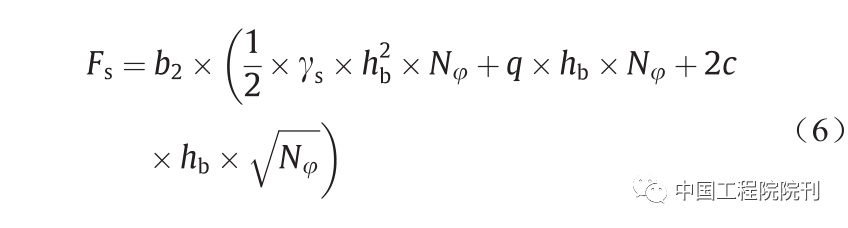
式中，q是轮缘在月壤上的压应力，q = P/A；N_φ是土壤的流值， N_φ = tan² (45° + φ/2)。由式（1）至式（6）进行推导，车轮F_d 的最大牵引力可以用等式（7）表示为：

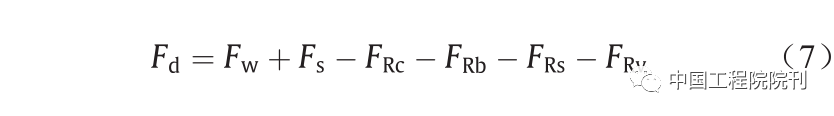
（二）优化参数确定

叶片弹簧优化是本文做出的主要设计，叶片弹簧优化可以有效提升系统的整体性能。优化方法为将叶片弹簧刚度k和弹簧初始扭矩T₀作为优化变量，使车轮能够在降低能耗的同时应对多种路况。

其他优化参数还包括：车轮在月壤上行进时叶片插入土壤的深度的最小值h_b、车轮滚动阻力产生的转矩T_f、支持力F_v和车轮摩擦力F_p。其中一些参数用作优化约束，而其他参数用作优化的输入函数。在计算上述参数时，主要基于以下路况分析：土壤通过性设置为高、中、低；斜坡角度变化从0°到30°。

通过对月壤参数、车轮参数和车轮倾斜阻力F_Rs（表1）的计算，我们可以获得在月壤不同通过性和不同坡度下叶片的最小插入深度h_b。然后将先前获得的车轮压力P（表1）和h_b与车轮阻力带入式（1）、式（2）、式（4）计算，得到车轮滚动阻力。将车轮阻力乘以车轮半径R 即可获得车轮滚动阻力产生的转矩T_f。表3列出了前轮相关的优化参数。

四、新型车轮的优化设计和实验

如图7所示，叶片5（i = 5）是车轮最底部叶片，也是与土壤直接作用的叶片。因此，在以下分析中将以叶片5的伸长量为主分析。叶片5的伸长量可以表示为 L_o5 (θ_s = 0) = L_oi (i = 5, θ_s = 0)，其中，L_o5的计算方法在 Appendix A中说明。同时，对叶片弹簧优化的目标函数如下。

（1）高土壤通过性要求：L_o5  (θ_s) ≥h_b (θ_s), θ_s= 0°, 5°, …, 30°。

（2）运行中的阻力能耗要求：最小为Σ[L_o5  (θ_s)−h_b (θ_s)]。

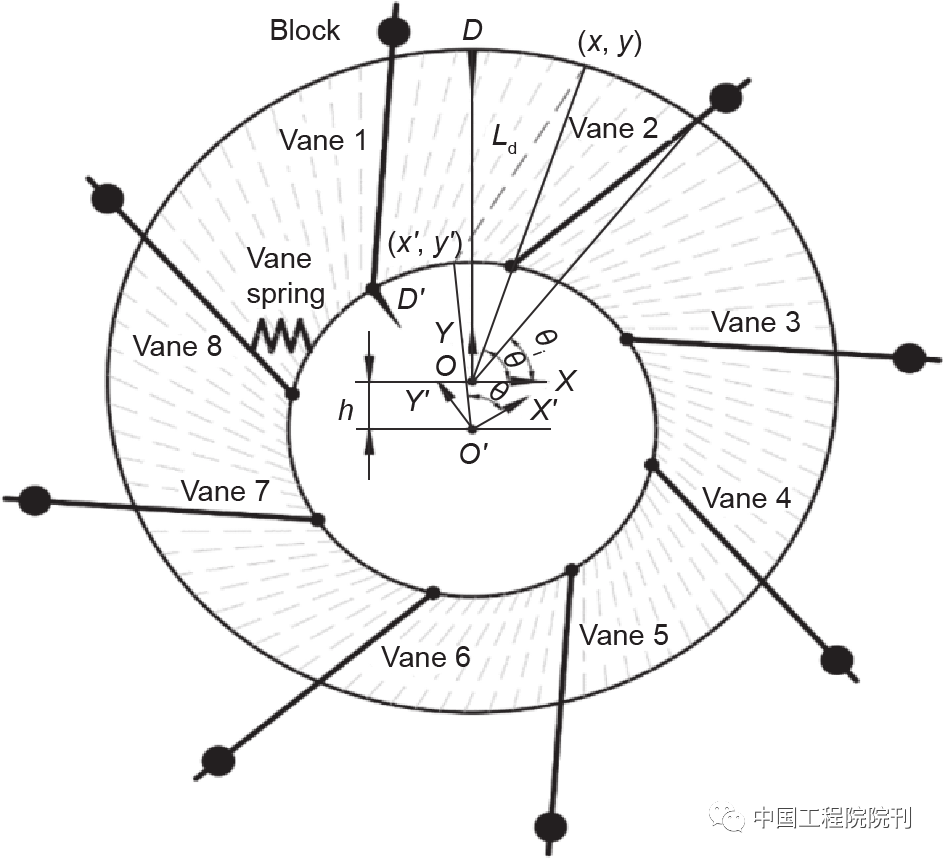
图7 叶片弹簧位置示意

（一）叶片弹簧设计优化

将在上文中获得的优化参数（包括T_f、F_p、F_v和 h_b）引入上述目标函数中，获得式（8）：

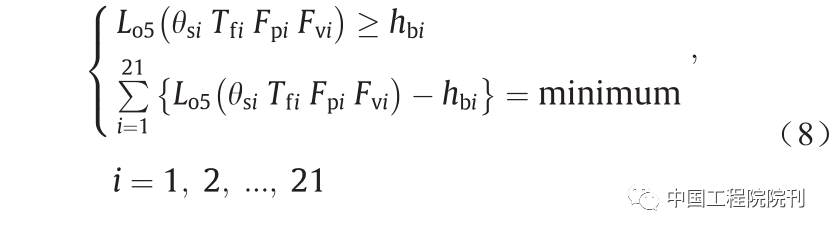
式中，i 代表道路状况，共21种，由不同坡度（θ_s = 0°, 5°, 10°, 15°, 20°, 25°和30°）和土壤特性（高、中、低）组成。通过：

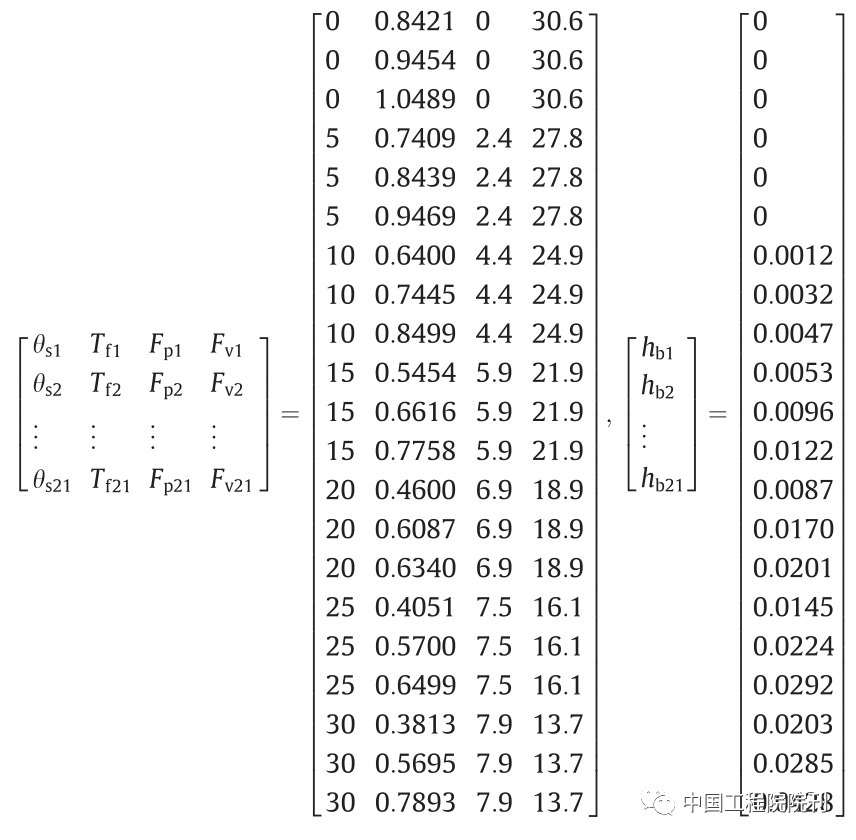
计算可得前轮叶片的弹簧刚度k和初始转矩T₀。

根据该计算，k＝0.112 N·m·rad⁻¹，T₀＝–0.038 N·m。在此，可为前轮设计一种弹簧，以确保在复杂的月球环境下的通过性。同时也可减少因叶片过度伸长产生不必要的能量消耗。中、后轮使用同样方法设计优化，本文在此不再详细说明。

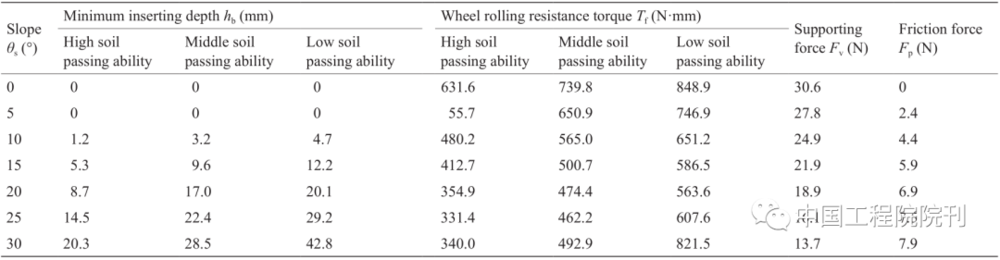
表3 前轮优化参数

（二）优化效果分析

在函数L_o5中，滚动阻力矩T_f和车轮摩擦力F_p总以关系T_f+R×F_p整体出现。所以可以将T_f + R×F_p视为变量，称为滚动摩擦力T_v。因此，初始函数L_o5中的三个变量可以以两个变量T_v和F_v的形式表示。为了分析前轮优化后的机械性能，将k = 0.112和T₀ = –0.038引入函数L_o5 (k, T₀, T_f , F_p, T_v)，可以获得h_b、T_v和F_v之间的关系。

图8示出了对于不同坡度（θ_s ＝ 0°, 5°, 10°, 15°, 20°, 25°和30°）的L_o5、T_v和F_v之间的关系。可以看出，当T_v和F_v较小时，叶片不伸出。当T_v和F_v达到一定值时，叶片开始伸长，并且随着T_v和F_v的增加，叶片进一步伸长。在图8中，不同的颜色表示不同的斜率，但它们并不吻合。这种情况主要是由于车轮和斜坡之间的接触点发生了变化。

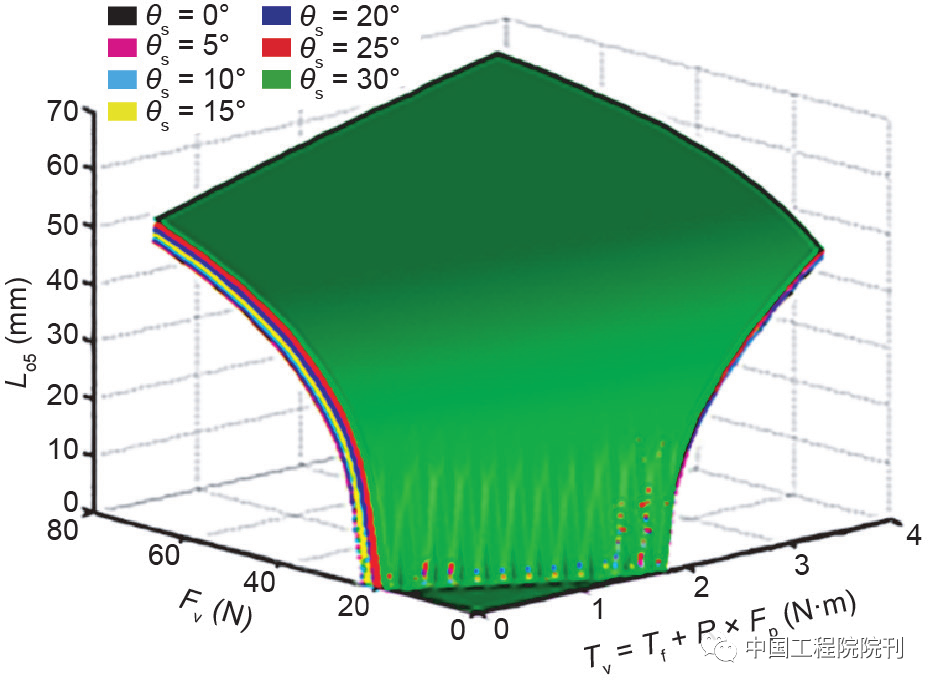
图8 不同坡度下L_o5、T_v、F_v的关系图

图9示出了延伸长度L_o5和插入深度h_b之间的关系。插入深度h_b有21个值。可以看出，每个值不超过其对应的表面，这意味着h_b≤L_o5。这表明叶片伸缩式步行轮可以顺利通过21种路况。此外，这21个值中的最大值与相应同色的表面接触，说明车轮已经将能耗降至最低。

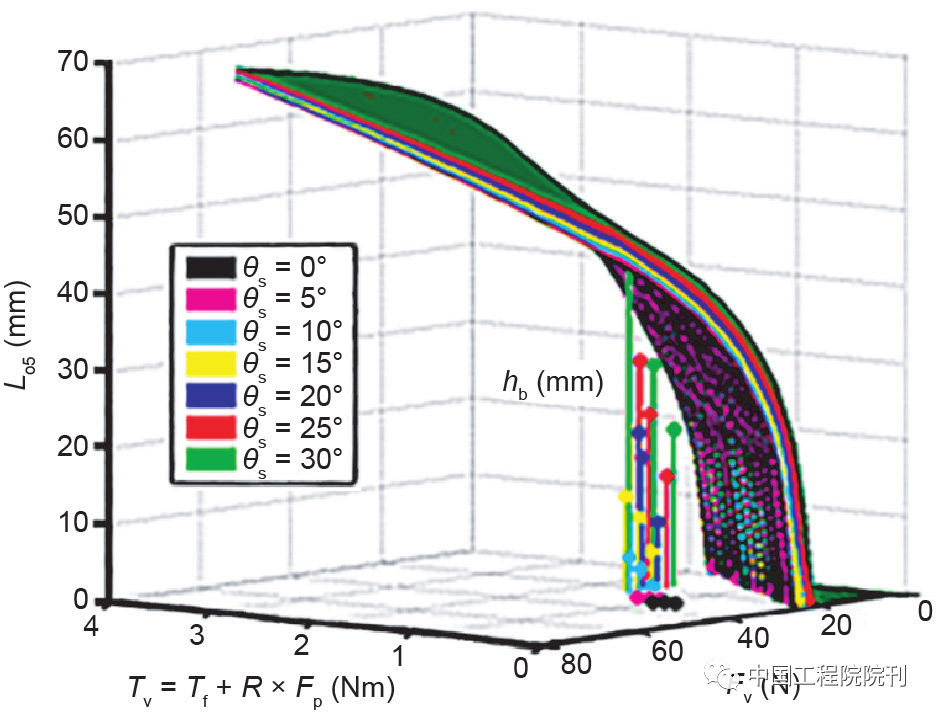
图9 L_o5与h_b的关系图

使用相同的优化方法，可得中轮的弹簧刚度k = 0.135 N·m·rad⁻¹，初始扭矩值T₀ =–0.023 N·m，后轮的弹簧刚度k = 0.218 N·m·rad⁻¹，T₀ =–0.128 N·m。

（三）叶片伸缩式步行轮原型机实验

为了测试叶片伸缩式步行轮的实际性能和可靠性，本研究组制造了具有相同尺寸的叶片伸缩式步行轮原型机，并将其安装在月球车原型CJ-1上（图10）。在中国空间技术研究院的月面模拟测试场上进行了模拟实验（图11）。

图10 CJ-1实验模型

图11 真实月面环境模拟

在测试过程中，当月球车在月壤中正常行驶时，叶片伸出长度正常增加以保持适当推力，如图12（a）所示。之后使用300 N的水平力拉动车轮以模拟月面阻力。叶片继续伸长，同时车轮牵引力增加。此时增大的牵引力可抵消水平拉力，由此原型机可以保持原速行驶，如图 12（b）所示。当水平拉力降低时，叶片长度逐渐恢复，能耗也逐渐降低，如图12（c）所示。

实验结果表明，优化后的叶片伸缩式步行轮可以根据地形阻尼控制叶片的伸长量。此外，当月球车经过复杂的道路时，其能耗可以被控制。

图12 叶片实际伸长情况

五、总结

本文提出了一种新型叶片伸缩式步行轮。这种全新的步行移动系统设计方案可以为解决月球车在月表行驶时面临的通过性以及能耗问题提供有用参考。本研究的主要结论通过数值模拟和仿真系统测试实现。

首先，本文建立了一个实验原型以分析现有的机械设计。在CJ-1月球车原型的基础上，针对月球上的复杂地形，设计提出了一种适配新型正反四边形悬架的叶片伸缩式步行轮。之后，本文对车轮的动静力学进行了分析。此外，本文对叶片伸缩式步行轮进行了参数分析并进行优化和仿真。最后，通过在实验室建立一个月球仿真环境证明所提出的新型车轮系统的有效性。

在未来的工作中，我们旨在建立一个更真实、更全面的试验场来模拟月球表面环境。如添加更多类型的月壤，以使实验能够尽可能全面模拟月球表面上车轮的实际行驶情况。另一个可能的扩展是增加车轮的承载能力以供未来载人登月车使用。嫦娥项目是“国家重点工程”的重要组成部分，本研究将为新型的月球车设计提供参考。我们同时还希望与来自世界各地的研究人员进行学术交流。

注：本文内容呈现略有调整，若需可查看原文。

原文：

Lu Yang, Bowen Cai, Ronghui Zhang, Kening Li, Zixian Zhang, Jiehao Lei, Baichao Chen, Rongben Wang.Mechanical Analysis and Performance Optimization for the Lunar Rover’s Vane-Telescopic Walking Wheel[J].Engineering,2020,6(8):936-943.

本文来自微信公众号：中国工程院院刊（ID：CAE-Engineering），作者：杨璐，蔡博文，张荣辉，李克宁，张子贤，雷洁浩，陈百超，王荣本