一位数学本科生的极限探索

本文来自微信公众号：原理（ID：principia1687），作者：佐佑，头图来自：unsplash

一

在今年5月，在论文预印网站arXiv上出现了这样一篇论文，内容是有关于组合学中最重要的一个问题——拉姆齐数。论文的作者名叫Ashwin Sah，他才刚刚年满21岁，如今是麻省理工学院数学系博士一年级的学生。

出生并长大于美国的波特兰市。他自幼便表现出对数学的喜爱，曾在高中时作为美国代表队的一员获得了2016年国际数学奥林匹克竞赛的金牌。他所感兴趣的数学领域有组合学、解析数论、傅里叶分析和无规矩阵理论，并对经济学、博弈论和人工智能感兴趣。| 图片来源：AMS

当Sah还是一名本科生时，就已经发表了许多数学结果。有数学家评论说，以Sah在本科时期所作出的学术成果的数量和质量，就已经足以让他获得教职。即使是在一个时有天才出没的领域，这样的成就也是罕见的。

二

我们将目光放回到5月的篇论文上，如前面说到的，这是一篇与拉姆齐数有关的证明。那么什么是拉姆齐数呢？

拉姆齐数所考虑的是涉及到被称为“单色团”的概念，这一概念描述的是在按照特定的着色程序为一张图（由边连接的点的集合）着色之后，由相同颜色的边相互连接的顶点个数。它由英国数学家弗兰克·拉姆齐（Frank Ramsey）于上世纪20年代提出。我们可以通过一个实例来更直观地理解何为拉姆齐数。

先来看一个有着5个顶点的图，将它们的每一个点都用边两两相连，如此一来，这5个顶点可用10条边连起来，形成一张被数学家称为完全图的图。接着，将每条边涂成红色或黄色两种颜色。现在问题来了，你能有办法避免出现3个顶点是用相同颜色的边连接而成的情况吗？

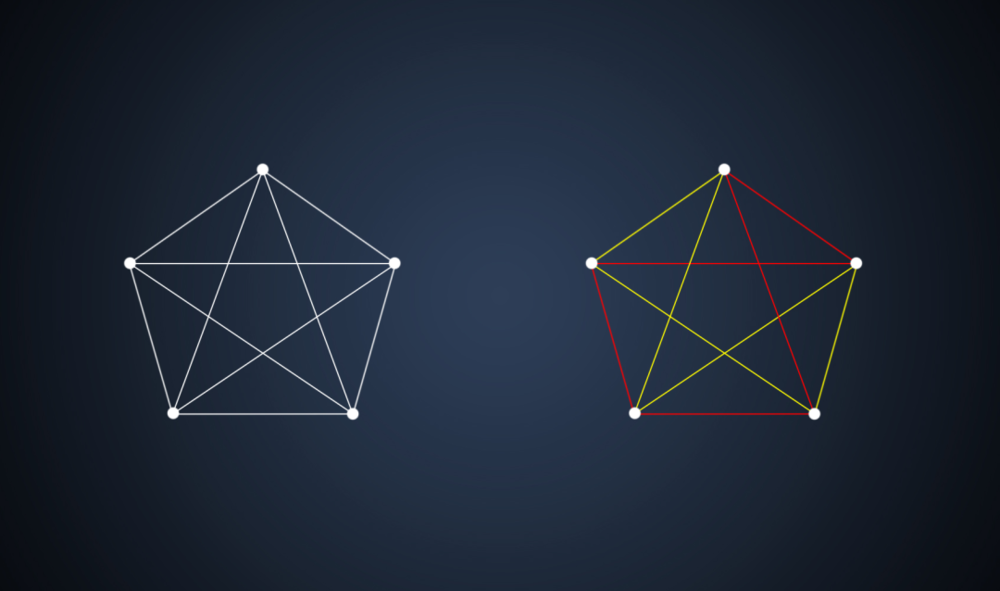
 对于由5个顶点连接而成的完全图来说，用两种不同颜色为其边着色，是有可能避免出现3个顶点由相同颜色的边连接而成的情况的。

对于有着5个顶点的完全图来说，这个问题的答案是肯定的。但当顶点数量增加到6时，情况就不同了。

对于存在6个顶点的完全图，我们需要用15条边来让每个顶点两两相连。当我们试图给这15条边分别涂上红色或黄色时，无论采用何种方法，都不可避免地会得到3个被相同颜色的边相互连接的点。

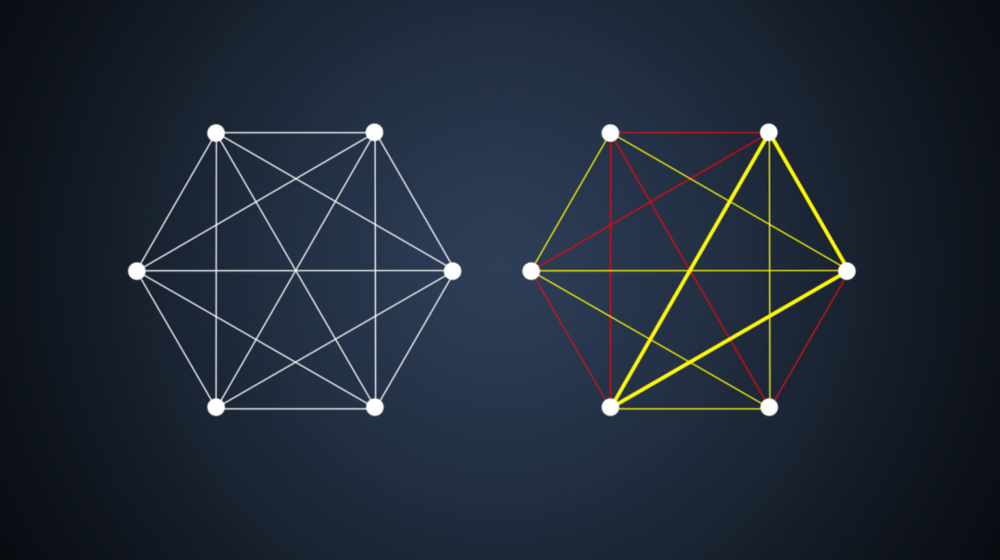
 对于由6个顶点连接而成的完全图来说，用两种不同颜色为其边着色，必然会出现3个顶点由相同颜色的边连接而成的情况。

这些被同一种颜色相连的点就被称为“单色团”。用数学家的话来说，对于颜色数量为2和一个大小为3的单色团来说，拉姆齐数为6。它意味着你需要一个至少包含6个顶点的完全图，才能保证这样一个单色团存在。

三

拉姆齐数的变化取决于用于着色的颜色的数量，以及你所设定的单色团的大小。随着“团”的大小越来越大，拉姆齐数的精确精算变得异常困难。因此，目前已经精确知道的拉姆齐数非常少，除了少数的一些较为简单的情况之外，在绝大部分情况下，数学家无法直接计算拉姆齐数，只能给出一个可能的取值范围。举例来说，即便是在看起来较为简单的情况——颜色数量为2、单色团大小为5，数学家也只知道相应的拉姆齐数介于43到48之间。

这种通过计算拉姆齐数的可能取值范围的方法最早可追溯至上世纪30年代，数学家保罗·埃尔德（Paul Erdös）和乔治·塞克勒斯（George Szekeres）最先提出了一种利用“上界”和“下界”的概念来研究拉姆齐数问题的方法。他们不对拉姆齐数进行精确计算，而是确保一个任意大小的团的拉姆齐数一定大于某个数（即下界）、小于另一个数（即上界）。

这种方法被后来从事这一研究的数学家所使用，只是一直以来鲜少出现令人瞩目的重大进展。2009年，加州理工学院的数学家David Conlon计算出了两种颜色的拉姆齐数的最佳上界（今年9月，Conlon于arXiv提交了一项新的研究，为多种颜色情况下的拉姆齐数给出了最佳下界）。而Sah在最新论文中，他采用与Conlon相同的方法，进一步改善了这一上界，成功证明了一旦一个图达到一定大小，那么它将无可避免地包含一个大小与图的大小相应的团。

 Sah在arXiv上传的论文。| 图片来源：arXiv.org

在接受媒体采访时，Conlon评论道，Sah的证明将这种方法推到了其极限。

四

Sah所作的工作难度非常大，且极具独创性。因此，他能在本科时期就取得这样的研究成果，是十分令人惊叹的。10月29日，专门针对在数学领域表现优异的美国、加拿大和墨西哥大学生的摩根奖，授予了正在麻省理工学院数学系攻读博士学位的Sah和另外一名学生Mehtaab Sawhney，以表彰他们在本科时期在组合学、离散几何和概率等领域中所作出的杰出成果。

参考来源：

https://www.quantamagazine.org/new-math-proof-raises-lower-bounds-of-graph-randomness-20201104/

https://www.quantamagazine.org/mit-undergraduate-math-student-pushes-frontier-of-graph-theory-20201130/

https://arxiv.org/abs/2005.09251

https://www.ams.org/news?news_id=6435

本文来自微信公众号：原理（ID：principia1687），作者：佐佑