

扫码打开虎嗅APP
本文来自微信公众号:中国科学院国家天文台(ID:NAOC-BJ),作者:陈云、蔡彦川,轮值主编:李然,责编:袁凤芳,编辑:赵宇豪、柒柒,头图来自:pexels
争论中的诞生
20世纪初,爱因斯坦发表广义相对论之后,科学届就宇宙的状态产生极大争论:宇宙究竟是静态的,正如爱因斯坦当时所认为的那样;还是动态的,如俄国物理学家亚历山大·弗里德曼(Alexander Friedman)1922年根据广义相对论提出的理论所预言的那般。这场关乎人类对宇宙基本状态的争论将由实验观测来分晓。
1929年,美国天文学家爱德温·哈勃(Edwin Hubble)基于一批“河外星云”(Extra-Galactic Nebulae)【注1】的观测公布了一项重大的发现:星云的视向退行速度v与其距离D之间大致成正比关系[1](图1), 即v = H0×D。这表明距离我们越远的星云,退行速度越快,进而表明宇宙是在膨胀的,宇宙是动态的。哈勃的发现因此被公认为宇宙膨胀理论的第一个观测证据。v = H0×D被称为哈勃定律,载入宇宙学教科书, 而其中的比例系数H0则被称为哈勃常数,它代表当前宇宙一个单位距离的膨胀速度。
宇宙膨胀的事实无疑打开了人类认识宇宙的新编章,宇宙大爆炸理论也在随后近百年中发展,并得到了更多的观测证实。
需要指出的是,早在1927年,哈勃发表他的结果两年前,比利时牧师,宇宙学家乔治·勒梅特(Georges Lemaitre)就在一篇文章[2]中理论上推导出星体的退行速度与其距离成正比,即后来公认的“哈勃定律”。可惜的是,Lemaitre 1927的文章发表在法语期刊上,大部分的英语世界未能在第一时间看到他的结果。虽然该文章在1931年被翻译为英文,发表于英国皇家天文学会月刊[3],但已经迟于哈勃的文章两年。哈勃1929的观测文章并无引用Lemaitre 1927(或者Friedman1922年[4])的文章。英译版本漏掉了法语版中几个关键的细节,也可能部分导致Lemaitre的结果不如哈勃的广为人知[5]。
2018年,国际天文学会(IAU)表决通过,改Hubble Law为 Hubble-Lemaitre Law。至此,经过了将近一个世纪,Lemaitre的地位得到了一定的认证。但IAU的动议本身也受到不少争议[6]。关于科学贡献的评价问题牵涉到诸多复杂社会因素,争论恐怕还会持续下去。
科学史上诸多的重大突破,都是基于整个科学群落的长期积累,形成了突破的条件和环境,进而由少数的科学家或者团队在恰当的历史时期去完成封笔之作。
打个不太恰当的比方,正如一群画家合作创作一个巨幅画像,完成最后点睛之笔的人固然对于画像的成型十分重要,但其他人的贡献也无可否认。哈勃的观测发现也不例外,在哈勃的观测结果之前,科学界对宇宙膨胀已经有明显的预期(比如Friedman1922, Lemaitre1927),在这个意义上看,他们,以及整个参与这方面研究的科学家群落在探索宇宙膨胀的道路上都值得敬佩。
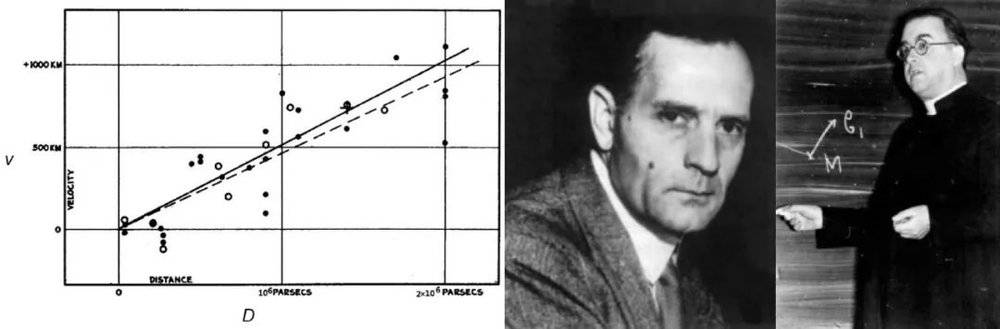
图1. 反映遥远星系的退行速度v与它们离地球的距离D成正比关系的定律,v = H0×D(左图,来自参考文献[1]),在2018年10月经国际天文联合会表决通过由原名哈勃定律改为哈勃(中图)–勒梅特(右图)定律, 以表示认可梅勒特在发现这一定律方面的贡献。
懵懂多变的婴孩期
哈勃常数是现代宇宙学模型的一个关键性基本常数:H0=v/D,速度除以距离,它代表当前宇宙的膨胀速率,也直接关乎宇宙的年龄(1/H0为时间,直接给出宇宙年龄的一个数量级估计)。因此,自1929年以来,研究者们都在为不断提高H0的测量精度而努力。
测量H0看起来十分简单,小学生都能做,我们只需测量某个遥远星体相对我们的退行速度v,以及它与我们的距离D,就可直接用他们的比值v/D得到H0。事实上,这正是哈勃1929年所做的,只不过,他不只用了一个,而是24个“河外星云”对H0给出限制以缩小误差。但事实证明,H0的测量十分具有挑战性,1929年至20世纪末这段时期,天文届公认的哈勃常数测量值一直在发生大幅度变化,并且颇具争议。主要因为我们对于遥远星体的距离D的测定十分困难。
哈勃在1929年估算出 H0=465±50 km/s/Mpc,勒梅特1927年给出的估计在误差范围内也算接近。根据这个值推测出的宇宙年龄约为20亿年,而当时地质学家利用岩石中放射性同位素的衰变估算出的地球年龄约为30亿年,宇宙年龄小于地球年龄,这显然是不合理的。宇宙年龄反比于H0,由此可见哈勃当初给出的H0值太大。1952年,德国天文学家沃尔特. 巴德(Walter Baade)宣布他测得的H0值约为哈勃当初所测值的一半,变化的关键在于星系的距离测定。
哈勃当年是在假设所有造父变星都是经典型的情况下利用其周光关系【注2】确定星系距离的,而巴德通过观测发现造父变星也存在两种不同的类型——经典型和第二型[7],并且两种造父变星遵循不同的周光关系。巴德通过这一修正将H0的值降了下来,从而解决了宇宙年龄与地球年龄之间的矛盾问题。20世纪后期,哈勃常数H0的估计值在不断下降。
这期间最有名的事件是杰拉德·德沃古勒(Gérard de Vaucouleurs)与阿伦·桑德奇(Allan Sandage)两位天文学家之间所进行的长久争论,前者坚信H0的值约为100 km/s/Mpc,而后者则认为H0的值会低至约50 km/s/Mpc。
和谐美好的发展期
21世纪伊始,合理且被广泛认同的H0测量值终于出现了。2001年,美国天文学家温蒂·弗里德曼(Wendy L. Freedman) 领导的哈勃太空望远镜重点项目 (HST key project) 团队根据近邻宇宙中(通常指红移小于0.1或0.15的范围内)造父变星和Ia型超新星距离的观测估算出H0=72±8 km/s/Mpc[8] 。这一数值刚好介于德沃古勒和桑德奇的结果之间,这才终结了德沃古勒团队和桑德奇团队之间的争论。
随后,来自早期宇宙的观测结果大致上支持Freedman在近邻宇宙测量,进一步肯定了科学界对H0约为70km/s/Mpc的信心。
对于早期宇宙,哈勃–勒梅特定律所描述的线性膨胀行为失效,宇宙学距离依赖于宇宙学模型。基于1998年宇宙加速膨胀的发现所建立的标准宇宙学模型[9,10],使得科学家能利用高红移的距离—红移数据来测定哈勃常数。
人类现今所能观测到的最遥远的信号则是来自于大爆炸的余晖——宇宙微波背景(CMB)辐射。我们所测量到的CMB辐射揭示了宇宙诞生约38万年之后的物质分布,这一数据包含大量的信息,可以用来测量诸多宇宙学参数,包括暗物质、暗能量和哈勃常数,前提是我们必须假定一个宇宙学模型。
但从另一个角度来看,用CMB的数据测量哈勃常数,从方法到数据都与近邻宇宙的测量完全独立,能用如此相互独立的实验来测量同一个物理量,再理想不过了。
21世纪之初最著名的CMB观测卫星便是NASA于2001年6月发射升空的威尔金森微波各向异性探测器(Wilkinson Microwave Anisotropy Probe,简称WMAP)[11]。WMAP在2003年公布了第一批观测数据,随后又在2007年、2009年和2013年初公布了后续观测数据,该项目基于CMB观测和标准宇宙学模型所估算的H0值与近邻宇宙观测所给出的值始终是基本相符合的。
这样的结果让诸多物理学家叹为观止:两组完全独立的实验,独立的数据,并且,数据本身跨越了上百亿年的宇宙历史,得到的结果居然是吻合的。如果这一结果为真,我们不得不为宇宙的和谐(标准宇宙学模型)而叹服;我们也有理由敬佩人类在科学测量的精度和准确度上的伟大成就。这一时期可视为 哈勃常数和谐美好的发展期(图2)。
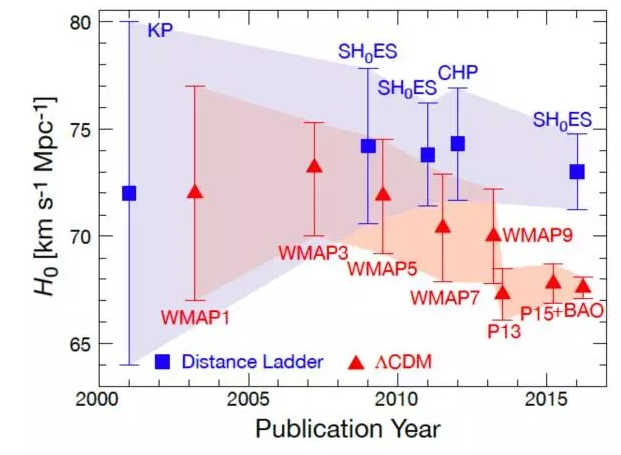
图2. 哈勃常数和谐美好的发展期(2001年-2012年)。该图展示了2001年至2016年期间H0的测量值;横轴是年份,纵轴是H0的测量值;其中蓝色带误差棒的点表示来自近邻宇宙观测所给出的H0值,而红色带误差棒的点则表示高红移观测所给出的H0值。可见在P13(表示普朗克卫星在2013年公布的结果,后面会提到)这个点之前,蓝色和红色区域都是相互兼容的(图片来自:参考文献[12])
矛盾频出的今朝岁月
在当今所谓的“精确宇宙学”时代,随着测量精度的步步提高,哈勃常数的测量准确度再次出现极大的争议。
2013年重磅来袭!WMAP组于2012年底刚公布完他们的最后一批观测,普朗克(Planck)卫星工作组随后便于次年3月公布他们在标准宇宙学模型框架下基于CMB观测数据给出的结果为H0=67.9±1.5 km/s/Mpc[13],这一结果比亚当·瑞斯(Adam G. Riess)团队于2011年基于哈勃望远镜对近邻宇宙的观测所给出的值H0=73.8±2.4 km/s/Mpc[14]略低。
早期宇宙的数据似乎倾向一个膨胀稍慢的宇宙(H0~68),而近邻宇宙的直接测量倾向一个膨胀稍快的宇宙(H0~73)。粗看,两大项目组所测得的H0数值似乎差不太多,都接近上个时代的70左右,但由于他们误差范围比之前缩小好几倍,事实上他们的差异已经十分突出,统计上已有3个标准差的差异,也就是说,两个结果一致的概率小于0.3%。
这一事件很快在天文学界掀起了一场热议。随后几年,两个项目组都在不断审查更新各自的测量结果,甚至相互检查对方的错漏,然而,呈现出来的问题并无缓解,反而越来越严重。
两组值的差异从之前的3个标准差上升到了如今超过4个标准差,一个向左走、一个向右走,渐行渐远(图3)。Riess团队于上月初(2021年12月初)发布的预印本文章[15]中给出的最新分析结果显示两组值的差异已上升到了5个标准差。可见,两者不同已是不可避免的事实。

图3. 哈勃常数矛盾频出的岁月(2013年至今)。左图展示了近几年公布的H0测量值,其中红色带误差棒的点表示低红移观测所给出的H0值,蓝色带误差棒的点则表示高红移观测所给出的H0值(图片来自:参考文献[16])。这两组值的分布和走势很容易让人联想到绘本漫画家几米笔下的《向左右·向右走》
争论的可能结局
过去几年,科学界对H0问题的讨论和关注可谓如火如荼,几乎每个星期都有论文在这一领域发表,作者们往往试图解决,或者声称解决了这一矛盾。但截止到2021年圣诞节前夜,这个矛盾依然未得到公认的解决。那么,早期宇宙数据对H0的限定与近邻宇宙的直接测量结果不一致意味这什么呢?大致的可能性有三:
第一:Planck数据,或者近邻宇宙测量的数据,以及他们分析过程可能存在问题。这个嫌疑恐怕很难被彻底排除,因为两个领域的观测和数据分析都极为复杂,都是一个团队,而不是某一个人,按照一定的流程分析处理得到的结果,这个过程原则上可以被100%重复,但实际上无人100%重复过。大部分的重新检验总是集中在最可能出现问题的方面,带有检查者的先验判断。如果有我们意想不到的误差因素,就很难被究查出来。
事实上,Planck团队和Riess团队已经有好几次尝试对自己的分析做深度排查,也多次质疑过对方的分析,但结果都没有发现明显的问题。所以,数据和数据分析过程的大问题至今没有发现,也难以100%被排除,估计更加深度的排查还会继续。
第二:两边的数据分析都没问题,是现有的宇宙模型有问题,我们对物理的理解有问题。这是有可能的,但这个可能性一时也很难证实或者证伪。诚然,标准宇宙学模型是联结早期宇宙与晚期宇宙的桥梁,用CMB数据得到的H0是带有模型假设的,质疑标准宇宙学模型者往往提出修改宇宙的膨胀历史,使得宇宙在早期的物质分布符合CMB的数据,而晚期膨胀稍快,这样就有可能让CMB的数据同时也与晚期宇宙直接测量的膨胀率相符合,譬如修改引力模型或者提出早期暗能量模型,此类模型不在少数,往往通过引进额外的自由度,使得新的模型能够在某个特殊的参数区间内与观测数据符合。然而,目前还没有某个修改标准模型的理论得到广泛的认可。
或许物理学的发展总是偏向于追求简洁和谐的美,基于广义相对论的标准宇宙学模型虽然还有许多悬而未解之谜,但它成功地解释了无数的观测数据,目前物理界似乎还没有找到足够的理由去接受其修改版本。
第三:我们还没有想象到的其它可能性。在物理学的发展史上,争论似乎是常态;它意味着问题的存在,而物理学的发展,往往也是从提出新的问题开始的。所谓真理越辩越明,争论很可能意味着下一次认识的突破。19世纪末的物理界也曾经认为当时的经典物理理论已经解释了所有的物理现象,只有两个例外,对于那两个例外的关注和讨论,后来直接导致了量子力学和广义相对论的发现,打开了人类认识世界全新的维度。
如今我们对于哈勃常数的争论,本身说明了这个问题存在,或许也是个难得的契机。相信对这个问题公开、透明、持续的讨论,将带给我们对宇宙新的认识。
★ 注1:当时哈勃和天文学界尚不知道银河系之外还有类似银河系的“河外星系”,因此哈勃称之为“河外星云”。
★ 注2:造父变星的亮度具有周期性的变化,并且,其变化周期与其亮度相关,所谓的“周期-光度”关系,或周-光关系,所以,我们只需测出造父变星的变化周期,就可以推知其绝对亮度, 进而知道它所处的星系与我们的距离。
参考文献:
[1] Hubble, E., (1929) "A relation between distance and radial velocity among extra-galactic nebulae". Proceedings of the National Academy of Sciences. 15 (3): 168–73.
[2] Lemaître, G., (1927) “Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques”, Annales de la Société Scientifique de Bruxelles, A47, p. 49-59
[3] Lemaître, G., (1931) “Expansion of the universe, A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra-galactic nebulae”, MNRAS, 91, 483L
[4] Friedmann, A. (1922), “Über die Krümmung des Raumes.” Zeitschrift für Physik, 10, 377-386.
[5] Livio, M., (2011) “Lost in translation: Mystery of the missing text solved”, Nature, 479, 171
[6] Kragh, H. (2018) “Hubble Law or Hubble-Lemaître Law? The IAU Resolution”, arXiv:1809.02557
[7] Baade, W. (1956) “The period-luminosity relation of the Cepheids”. Proceedings of the National Academy of Sciences. 68, 5-16
[8] Freedman, W. L., et al. (2001). "Final results from the Hubble Space Telescope Key Project to measure the Hubble constant". The Astrophysical Journal. 553 (1): 47–72.
[9] Riess, A. G. et al., (1998) "Observational evidence from supernovae for an accelerating universe and a cosmological constant". Astronomical Journal. 116 (3): 1009–38.
[10] Perlmutter, S., et al. (1999). "Measurements of Omega and Lambda from 42 high redshift supernovae". Astrophysical Journal. 517 (2): 565–86.
[11] https://lambda.gsfc.nasa.gov/product/map/current/map_bibliography.cfm
[12] Freedman, W. L., (2017) “Cosmology at a crossroads”. Nature Astronomy, 1, 0169
[13] Planck Collaboration, Ade, P. A. R., et al. (2014) “Planck 2013 results. XVI. Cosmological parameters”, Astronomy & Astrophysics, 571, A16
[14] Riess, A. G., et al. (2011) “A 3% Solution: Determination of the Hubble Constant with the Hubble Space Telescope and Wide Field Camera 3”. The Astrophysical Journal, 730, 119
[15] Riess, A. G., et al. (2021), arXiv:2112.04510
[16] Riess, A. G. et al., (2019), “Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM” , The Astrophysical Journal, 876, 85
本文来自微信公众号:中国科学院国家天文台(ID:NAOC-BJ),作者:陈云(中科院国家天文台副研究员,目前主要研究为lyman-alpha线丛的宇宙学应用、强引力透镜宇宙学、暗能量理论及观测检验)、蔡彦川(爱丁堡大学英国皇家学会大学研究员,主要研究涉及宇宙大尺度结构统计方法和观测),轮值主编:李然,责编:袁凤芳,编辑:赵宇豪、柒柒
