如何让机器人犯错误？

在我们人类的印象中，计算机已成为精确、高效的代名词，不仅应用广泛，能处理很多复杂问题，而且现在随着人工智能领域深度学习的进展，仿佛真的可以无所不能。甚至有人认为，假以时日，达到或超越人类的智能都不是问题。如果再给计算机 AI 装上身体，那么在科幻世界中的机器人种族就可以实现了。

但是你是否知道，计算机是如何做到精确、高效进行计算，处理各项任务的呢？让我们先回到现实和源头。不用担心，在“它们”成为“他们”之前，我们还可以好好认识下他们。本文来自微信公众号：Mindverse Research（ID：gh_be9d7092abf7），作者：十三维，原文标题：《如何让机器人犯错误？浅谈粒度计算》，题图来自：视觉中国

一、计算机何以精确

现有大多数计算机的系统结构都基于“图灵机”。图灵机是一种抽象的计算模型，也即一种数学模型。自从有了图灵机，人们才真正理解了“计算”的的含义，并且将人脑、计算机、甚至自然界中一切可归结为机械操作的过程都等价为了计算。

而图灵机正是一种最基本的计算模型，它由艾伦·图灵在跨时代的论文《论可计算数及其在判定问题中的应用》提出。

简单来说，图灵设想了一个带读写头的机器，它可以在一条无限长纸带上运动。

这个机器每运动到纸袋的一格，就会读取此格的信息，并且根据自己当前的内部状态，去查找机器内置好的一张程序表，找到这种情况下对应的指令并执行动作，比如更改自己的内部状态，将纸带格子信息涂改、前进或后退等等。

从上面图灵机的运作过程，我们看到图灵机的基本运作过程：

上面构成规则表的状态、输入信息、输出动作都是非空有穷集合，所以图灵机在归类上属于有限状态机（FSM）。图灵还规定，图灵机输入和输出的信息仅仅是 0 和 1 即可，因为这是最简单的信息。然而在原则上，它却能等价为任意复杂强大计算能力的机器。

这样我们看出，图灵机所做操作无非把 0 和 1 之间进行互相转换，而最简单的计算就是对 0 或 1 进行布尔运算（与、或、非）了，那么计算机科学家们就可以围绕二进制和作为基本规则的布尔代数，去制造最简单的可以物理实现的图灵机。

后来，另一位伟大的计算机科学家冯·诺依曼，就根据图灵机的基本原理，创造性地提出了把程序本身当作数据来对待存储程序原理，这就是冯·诺依曼体系结构，从第一台计算机 ENIAC 开始，所有计算机都是遵从图灵机模型和沿着冯·诺依曼体系结构的，直到最近神经形态芯片和量子计算机才开始有所改变。

至此，我们可以看到，图灵机基于经典集合论的模型，通过数学用 0、1 进行逻辑实现，精确描述，确定的集合范围。而计算机处理的过程，则是基于对二进制处理的布尔代数，也是抽象确定性的计算法则。

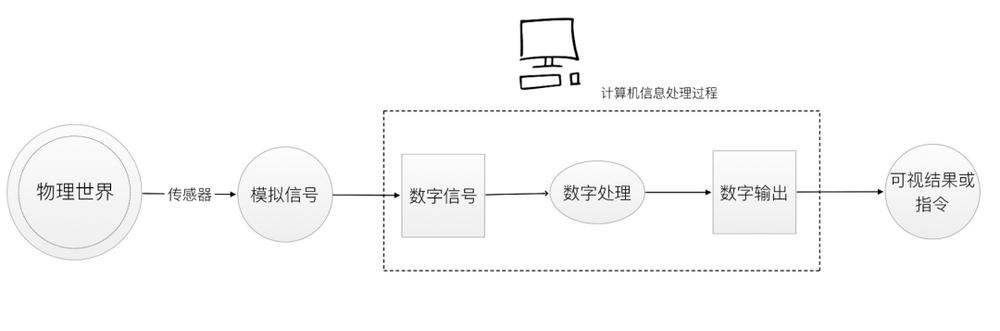
举个不太恰当的例子，现在的计算机就好像在吃掉被我们处理过的食物，我们已经提前为他们进行了清洗、切割、烹饪，然后它们得到这些结构化的数据后，就可以飞速进行吸收、处理、学习、增强、输出了。

有多少人工，就有多少智能——人工智能界现状

这样我们就理解了，计算机处理的信息，确切地说二进制比特，它本身就是精确的信息流。计算机如此精确，就是因为它们被人类封装到了一个几乎完美的比特环境中，并且遵守确定的计算规则，也就导致了它们的决策机制是确定性的、是远超于人类的高效。

而人脑则很不一样，对于感知信息与其它信息，通过脑中的生物神经网络，神经元既可以编码数码信号，也可以编码模拟信号能同时编码模拟信号和数字信号^[1][2]。并且，处理感知信息比符号信息更容易。

早期的计算机曾出现过模拟计算机，但效率和精确度太差，于是以图灵机和冯诺伊曼体系为模型的数字计算机大行其道，在摩尔定律下，速度越来越快，这就使得计算机成为了精确、高效的代名词。

那么，如何让计算机直接面对真实世界，处理充满噪音的自然信息，处理不精确性和不确定性的知识呢？

还是要向人类学习。这次计算机需要向人类学习的是通过“模糊性”去处理不确定性——曾经被认为人类面对计算机的最大劣势。

二、人类怎么面对不确定性

生活在物理世界的人类，都在面对哪些不确定呢？

• 真实世界的不确定，数据的不确定性，信号噪声

• 概念、术语的的模糊性

• 知识自身的不确定性，如规则的前后件间的依赖关系不完全可靠

这些不确定性，人类感官和大脑可以天然进行处理，但计算机却很难。

要让计算机能够处理以上事情，还必须让人类以身作则，用自己的大脑去教会计算机学习如何处理世界的不确定性和知识的模糊。

就像之前运用图灵机模型，将信息基于传统集合论和布尔代数逻辑去处理精确数据一样，数学家和计算机科学家开发采用了种种数学工具应对以上问题。进行处理，目前经过了三个阶段。

概率与统计

基于数学的概率论与统计，人们把其中贝叶斯方法应用于机器学习，并在后续发展出 D-S 证据理论。对于前者，贝叶斯深度学习虽然可处理小样本下不确定性预测问题，但是过于依赖先验概率，并且在最优假设下计算复杂度过高。

而 D-S 证据理论则进一步满足更弱化的条件，甚至不需要知道先验概率，通过引入信任函数的概念，形成了一套基于“证据”和“组合”来处理不确定性推理问题的数学方法，具备了直接表达“不确定”和“不知道”的能力，目前已经有了很大成果，广泛应用于专家系统中。

但是它缺点也是明显的，一方面要求证据必须是独立的，在证据合成规则上也缺乏坚固的理论支持，另一方面更重要是，它和贝叶斯方法一样，不能处理模糊和不完整的数据。

模糊集合理论

集合论是现代数学的基础，一切数学理论，包括前面所提到的图灵机模型，其运算规则布尔代数都是基于集合论建立的。

在经典集合论中，关于元素和集合之间的关系是确定的，一个元素和一个集合之间有一个确定的隶属关系，遵从逻辑上的排中律。比如 自然数 2，要么属于质数，要么不属于质数，不可能居中，或者亦此亦彼。但是在现实世界中，我们常常遇到这样的问题：比如，骡子究竟属于马还是属于驴？如何定义“胖”？忒修斯之船什么时候不是原来那艘船了？

这些界限不分明甚至是很模糊问题，都可以用“模糊数学”来解决。模糊数学通过引入模糊集合的概念，重新拓展了原来康托尔集合论的定义。

它对原来的集合，引入了一个到 ^[0，1] 区间的隶属函数，对集合中每个元素，都对应一个 0 到 1 之间的数值，也称隶属程度。对于经典集合论，元素和集合之间的隶属程度恒为 1。比如，一只小白马对马的隶属程度为 1，而一个150斤的人在中国隶属胖的程度则大约为 0.4，等等。

通过定义模糊集和隶属函数可以很容易表达客观现象界面不明的模糊状态，也通过引入语言变量轻松处理人类语言中的模糊概念，从而让计算机能够进行处理不不确定性和不精确性问题。尤其，人脑中的模糊处理机制，计算机也终于能够实现了。

在这方面，目前进展最大的是模糊神经网络（Fuzzy Neural Network），通过结合模糊理论和神经网络，现在的人工智能可以像人脑一样进行模糊识别、模糊学习、模糊决策、模糊控制等，在医疗、气象、心理等很多方面都取大了很大成功。

但是模糊集合理论同样也是有局限的，它虽然能让计算机处理模糊类数据，但却同样要求要提供附件信息或先验知识，即模糊集合中的隶属函数。而这些信息在很多情况下并不容易得到。

那么，有没有一种方法，无需提供问题所需处理的数据集合之外的任何先验信息， 就能对所针对问题的不确定性进行较为客观的描述或处理呢？

答案是有的。这次计算机向人脑学习的是“范畴化”（Categorization）能力。

当然，这次数学家们也进一步升级武器，提出了“粗糙集理论”（Rough Sets）。

粗糙集理论

通过粗糙集理论，类比于人脑对不同层次信息的处理，数学家和计算机科学家将数据和信息划分为不同的粒度（Granularity），并将其运用到计算机信息处理上，发展出了商空间理论和三支决策理论，这一新兴的计算领域被统称为“粒计算”，是当前人工智能研究领域中模拟人类思维和解决复杂任务问题的新方法，这种方法能使机器有效处理具有不精确性和不确定性的知识。

三、从模糊决策到粒计算

前面已经提到，计算机师从人类大脑，通过模糊集合理论，已经具备了模糊决策能力。只不过这种模糊识别分类能力，依然需要人类提供先验知识。

那么人类大脑是怎么获得这些先验知识的呢？

人类自诞生起，就面对一个千姿百态的物质世界，一个纷繁复杂的经验世界。因此，人类认识的基本任务必然首先是分类，否则不可能有效地存储和利用知识。

通过分类，不同的对象可以视为等同，这个分类的过程就是范畴化（Categorization）的过程。它是人类的一个关键性认知方式，范畴化的最直接作用是减轻认识过程中的工作负担，可以说是一个物种得以生存和进化的基础之基础。

只有当一个物种能区分谁是朋友，谁是敌人，就像我们人类祖先，能够区分谁是我们部落成员，哪些动物是危险的，哪些动物是可以食用的，我们人类这个物种才能存活下来。

而且不仅如此，人类的范畴化能力，还使得人类能理解抽象和具象的区别，即理解不同层次范畴之间区别，从而建立概念框架和语义系统，从而认识客观外界的复杂现象，理解各类事体之间的种种关系，从而对各类经验进行处理、储存、推理。

在上面所说，人脑对自然万物“范畴化”能力，这是认知语言学的概念，若换到数学和计算机科学，则是对不同信息和知识“粒度”的划分。

人类智能的一个公认特点，就是人们能从极不相同的粒度 （Granularity）上观察和分析同一问题。人们不仅能在不同粒度的世界上进行问题求解，而且能够很快地从一个粒度世界调到另一个粒度世界，往返自如、毫无困难。这种处理不同粒度世界的能力，正是人类问题求解的强有力的表现^[3]。

这段话的前部分是指人类的多粒度认知能力，而后部分是指人类动态粒度认知能力。

那么什么是粒度呢？在模糊集合理论之后，数学家们再一次高瞻远瞩，通过“粗糙集理论”给出了确切定义。

粗糙集理论是建立在分类机制的基础上的。知识即被认为是一种分类能力，人们的行为即是基于这种分辨现实的或抽象的对象的能力（即范畴化的能力）。

粗糙集理论将分类定义为在特定空间上的等价关系，即相差不大的个体被归于同一类，也称不可区分关系。等价关系构成了对该空间的划分。每一被划分的集合，即一种知识，是一种对数据的划分，也被称为“概念”。

举例子来说，对于所有人组成的空间，包括你、我、张三等全部人类个体对象。它可以分为家庭、家族、民族、种族等不同分类。对于家庭这种划分标准而言，你和你父母都属于同一个家庭，因此都是相互等价的、属于同一种等价关系。而你的家庭、我的家庭、张三的家庭……所有家庭组成的集合，则是所有人这个空间的组成知识的一个颗粒（Granule）。

当然，与此相应的，家族、民族、种族也都是一个知识颗粒，只不过粒度越来越大。

在原有的计算中，比如计算身高，对个体的输入通常就是一个数值。

而对家庭、家族则可以是一个身高区间，对民族、种族则可能是概率分布或模糊集合了，我们可以看出，这种以颗粒为研究单位的输入已不单纯是一个数值，而是表征一堆数据的某个指标。

这和我们人类处理信息过程很类似，比如一提到北欧人，我们印象身高会更高大，这就是人脑对北欧这个种族表征的结果，尽管你可能见过很多很矮的北欧朋友，但和种族是处于不同的颗粒度的，所以并不会影响你的直观印象。

四、一个粗糙集定义域分析的例子

在粗糙集可以用来处理不完整的信息，其中模糊的部分用边界集合來代表。

其中一个信息系统是四元组（U，P，V，f）定义的：U是对象集合，P是属性集合，V是属性的值域，f 是一种映射，反应对象集合之间的值；

其中我们感兴趣的对象组成的集合被称为论域，论域的任何一个子集（包括空集）称为知识，对论域进行分类的能力。一般由特征属性进行分类。

论域中互相不可分表的对象组成的集合被称为基本集。在某一知识下，如果论域可以由知识中的一个或者多个子集组合而成，那么就成为精确集，否则就成为粗糙集。

对属性集合P和全集U，其中任意一个不可区分关系：

显然，R ⊆ U×U。不可区分关系 R 代表我们对对象认知缺乏，不能将已知信息系统中的某些对象区分开。R 也被称为等价关系，则 （U，R）形成一个近似空间（Approximation Spaces）。

比如，若在动物中，以黑白为知识区分，那么黑色的狗和黑色的猫就是不可区分关系，也就是等价关系。

论域的划分构成粗糙集的一个近似空间，划分中的每一个分开成为一个知识粒度（Granules of knowledge）。在粗糙集中，等价类的力度越细，其划分能力就越强，近似集越精确。否则划分能力就弱，近似集越粗糙。

虽然我们对R缺乏足够认知信息，但如下图所示，我们却可以求出上近似集（The Upper approximation）和下近似集（The Lower approximation）。上近似是指包含给定集合 U元素的最小可定义集，下近似则是包含于U的最大可定义集。

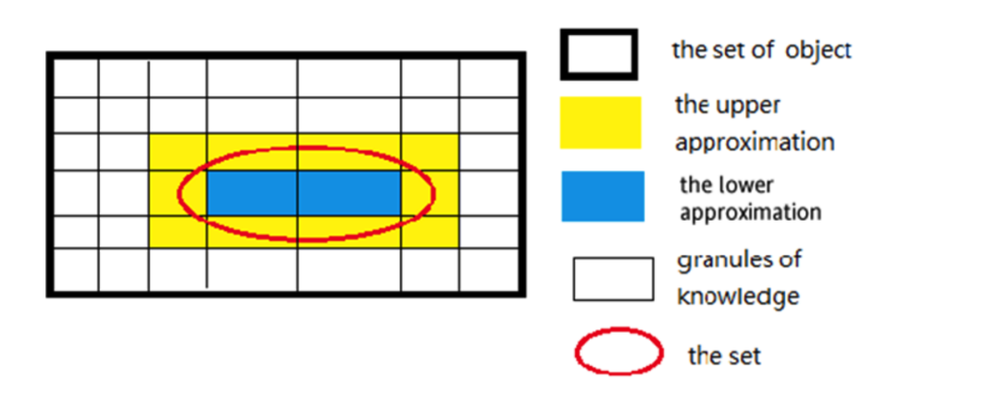
下面我们是一个有 （头痛、肌肉疼痛、体温、流感）不同症状属性病人的例子，其中 P1～P6 是不同的病患对象。

则 S = {P1，P2，P3，P6} 确定有流感：

The Upper approximation of S = {P1，P2，P3，P5，P6}

The Lower approximation of S = {P1，P3，P6}

P2， P5 不能用头痛、肌肉疼痛、体温来划分，因此是不可区分关系。在简化知识粒度进行规则推演，可以容易得到：体温高必有流感。 

在粒计算中，则可基于粒度空间，去解决最优聚类问题，即使面对海量不精确、不完整、不确定的数据，计算机依然可以自行学习进行不同粒度的区分，终于学得人脑千百万年来进化所得的“范畴化”大法。

粗糙集结合机器学习的聚类过程^[4]

五、从粒计算到模拟意识

上面我们讲到了计算机如何向人类学习“犯错误”，学习“模糊性”思维去做决策，学习如何对数据“范畴化”识别出不同的粒度，并在此基础上进行信息处理。

但是，现有的计算机，无论怎么在思维上怎么像人类，也只是止于知，所处理的依然是被喂好的数字信息，所在的依然是数字环境，那么，怎么让计算机真的像人，成为一个在真实物理世界自主学习的真正智能呢？

很简单，下一步继续模拟人类，不仅在软件上，而且在硬件上。

要让计算机有更大的能力，就必须从数字环境上释放出来，以机器人的具身形式直接面对真实世界。

在这方面，一些科技公司，已经取得了一定成功，比如 Willow Garage PR2 公司开发的 PR2 机器人，通过各种传感器直接接受物理世界信号，采取模糊决策控制，不需要重新编程就能学习新事物，比如玩乐高玩具。

但是科学家们还想走得更远。认知科学家们最新研究表明，人类的认知过程，是和身体、大脑高度相关的。身体、大脑的结构决定了生物的认知过程，因此，要让机器人实现真正具身的模拟，首先就要打破以往计算机“离身认知”的假设。这就是说，机器人的硬件组成，尤其是芯片，会直接影响软件系统的运作，因此就要重新考虑芯片架构。

前面已经提到，人脑的生物神经网络，既可以编码数字信号，也可以编码模拟信号。

而这些年，计算机科学家也开始尝试研究一直神经形态芯片并进行类脑计算，例如脉冲神经网络（Spiking Neural Network， SNN）进一步在硬件上模拟人脑，比如它不仅程序和存储不分离，处理本身和存储也不分离，如果应用在机器人中，就可以使得它结合各种模拟传感器，可以直接表征真实世界的模拟信号，而不仅仅是被二次处理过的数字比特。

这是模拟计算机和非冯诺依曼体系（non-Neumann computer）计算研究，还需要我们进一步探索。

我们可以看到粗糙集、粒计算以及相应的三支决策，可以和目前诸多技术结合起来，从物理学重整化到类脑芯片与类脑计算、从符号动力学学到 Jeff Hawkins 的千脑理论等等。

可以看到，计算机的发展之路，是一条越来越像人的道路。它不仅学习了人类如何像数学家那样进行精确计算与推理，还学习了人类如何模糊性处理知识，如何自发对不确定数据范畴化形成不同的知识粒度，以及如何以机器人具身形式和不确定性世界互动，通过不断试错，获得反馈自己学习知识。

甚至，计算机的“心”也越来越像人脑，不再是封闭的集成芯片，而是是一种输出可以变化的模拟芯片。甚至在未来，随着量子计算成熟，机器人会拥有更加强大的计算能力，还可能具备情感和自我意识。

粒计算和意识关系也很大。2021年一篇论文中认为，只有神经系统中某一粗粒尺度的信息才会在意识中得到反映^[5]

当然，这条越来越像人的道路，也有可能是错的，就像人类制造飞机飞行虽然遵循空气动力学，但并非像鸟一样挥动翅膀。但是不管怎样，在我们看到人工智能逐渐越来越像我们的过程中，我们一定会更加深刻认识到我们自身，并探索出一条真可行之路。

参考文献：

[1] Thorpe， SJ Spike arrival times: A highly efficient coding scheme for neural networks (PDF) 

[2] Eckmiller， R.; Hartmann， G.; Hauske， G. Parallel processing in neural systems and computers (PDF) . North-Holland . 1990: 91–94. ISBN  978-0-444-88390-2)。

[3] 《三支决策与粒计算》

[4] https://content.iospress.com/articles/journal-of-intelligent-and-fuzzy-systems/ifs162006

[5] Chang AYC， Biehl M， Yu Y， Kanai R. Information Closure Theory of Consciousness. Front Psychol. 2020 Jul 15;11:1504. doi: 10.3389/fpsyg.2020.01504. PMID: 32760320; PMCID: PMC7374725.

本文来自微信公众号：Mindverse Research（ID：gh_be9d7092abf7），作者：十三维