菲尔兹奖得主再突破：几个世纪的难题有了新进展

本文来自微信公众号：量子位 （ID：QbitAI），作者：Pine、萧箫，原文标题：《菲尔兹奖得主再次突破数论难题：多少整数能写成2个有理数立方和？结论直接影响“千禧难题”之七》，题图：2014年菲尔兹奖颁奖，左五为本次论文作者之一的Manjul Bhargava，来自：视觉中国

困扰数学界几个世纪的难题，终于有重大突破了！

这个难题如果被解决，会直接影响到一个著名未解之谜的求解——贝赫和斯维讷通-戴尔猜想。

贝赫和斯维讷通-戴尔猜想是数学界顶尖的7大千禧难题之一，有人为了证明它，悬赏过最高100万美元的奖金。

所以，究竟突破了什么难题？

求解一共有多少整数，能被写成2个有理数（整数和分数统称）的立方和。

例如整数13，就可以被“拆”成有理数7/3的立方、以及有理数2/3的立方总和：

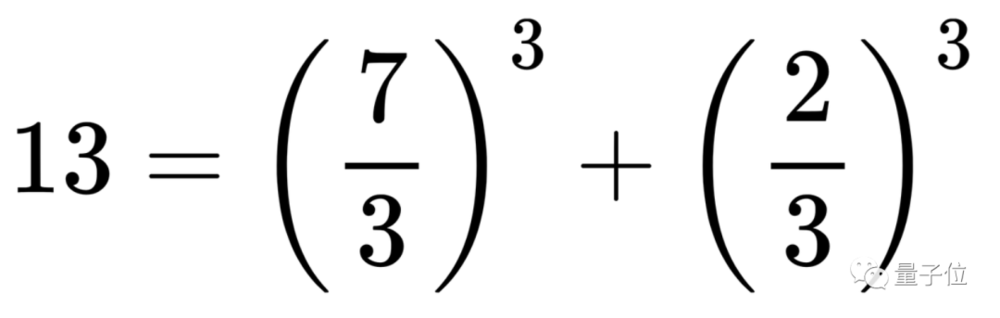
看起来似乎不难，但数学家们在这几百年来关于它提出的各种猜想，却没有一个被真正、彻底地证实。

普林斯顿高等研究所的数学系教授Peter Sarnak对此感叹：

分析两个数的立方和，意味着研究的族（family，集的同义词）非常小，族越小意味着问题越难。

我只能说这个问题很难、特别难，答案几乎“遥不可及”。

但对于学界而言，这个问题的求解又至关重要。它不仅是解决很多纯数学问题的核心突破口，在应用数学如密码学领域也颇受重视。

无证明，不数学。现在3位数学家再次朝这一难题发起挑战，并成功突破了关键瓶颈之一。

所以这个数学问题究竟难在哪里，数学家们又究竟如何取得了这一突破？

选择与三次方“死磕”

我们先来回看一下这个要解决的难题：究竟有多少个整数，可以表达成有理数三次方和的形式？

这时可能会有盆友好奇，为什么数学家们要死磕三次方的和，而不是平方、四次方、五次方……呢？

答案也很简单——它更难，也更有用。

具体原因有以下三点：

其一，除了三次方之外，无论是小于它的二次方、还是大于它的N（N＞3）次方，有些问题已经被解决过了。

就拿二次方来说，已经有非常具体的方法来判断哪些整数能成为两个有理数的平方和。

这个方法是在17世纪早期，数学家阿尔伯特·吉拉德（Albert Girard）和皮埃尔·德·费马（Pierre de Fermat）提出的，如果不符合这一条件，则整数不能用有理数二次方和表示。方法具体如下：

首先，将挑选的数字分解成质数幂的形式。以整数490为例，它可以被分解成下面这种形式：

然后，对分解后的质数进行检查：如果其中一个质因数除以4的余数为3，那么它的幂必须为偶数。只有这样，原来的数才能表示为有理数平方和。

这里7除以4余3，它的指数为2，符合偶数的要求，因此整数490可以用两个有理数平方和表示：

其二，基于上述条件，“能否被2个有理数立方和表示”也可能成为继奇数、偶数之外，又一个将整数有效分为两个阵营的分类方法。

毕竟数学家们推算过，发现能用有理数二次方和表示的整数比例很低，同理N次方（N＞3）也是。

相比之下，可以用三次方和表示的整数就非常丰富。

光是在1～100的整数里，就有59个能用两个有理数立方和来表示：

蓝色数字可以写成两个有理数立方之和

这样的话，大约就有59%的整数能被2个有理数立方和表示，甚至有数学家猜想这个数值能被推广到所有整数范围中。

其三，数学家们研究这个问题也不仅仅是为了有一个新的整数划分方式，它还和数论中的“热门研究领域”椭圆曲线有关。

椭圆曲线方程

椭圆曲线具有极其复杂的结构，这使它成为纯数学和应用数学等许多领域的中心，在密码学中也有很大的用处。

立方和问题，就是椭圆曲线中的一个特例。

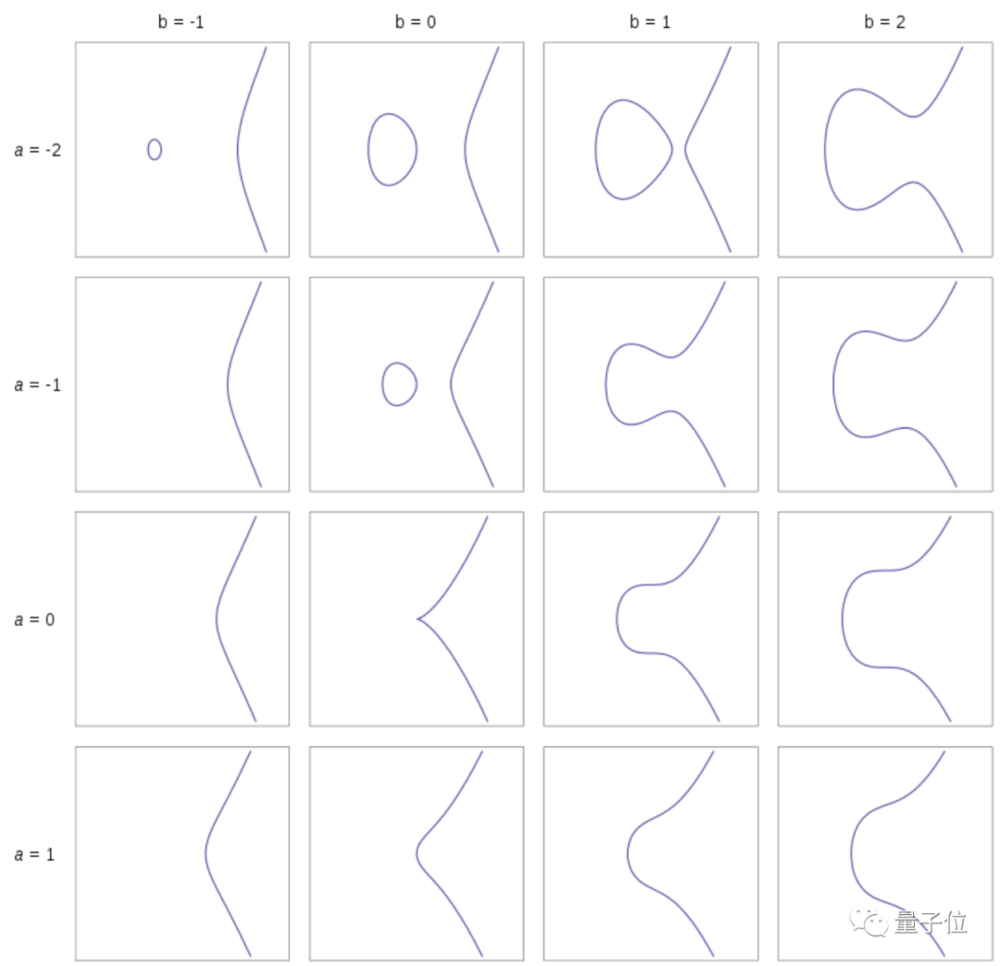
椭圆曲线，图源维基百科

如开头提到的贝赫和斯维讷通-戴尔猜想，就是椭圆曲线领域的一个核心问题。

如果这一猜想成立，便能推断出符合上面1~100整数表现（即蓝色数字图）的结论：

在1000万个数字中，约有59%是两个有理数立方的总和。

不过，上面提出的这么多推断，绕来绕去也都只停留在猜想层面。

过去的几百年里，不少数学家试图揭开这个谜题，但要么无法得出结论，要么无法证明自己的推断是正确的。

它不像指数为2时，整数可以轻松被证明能否被拆解为两个有理数平方和（方法如上），毕竟指数为3时，没有确切的方法可以证明整数能否被拆解。

但尝试一个个“暴力拆解”整数又是不现实的。因为在整个拆解过程中，涉及到的计算量巨大。毕竟相较于拆成两个整数立方和，拆成两个分数立方和的难度要大得多……

举个例子，整数2083虽然可以被拆解成两个分数的立方和，但光是这两个分数的分母，就长达40多个数字！这还仅仅是一个整数的计算量，更别提挨个儿计算其他整数了。

现在，终于有3位数学家成功突破了这个问题的瓶颈，第一次给出了可以拆解成两个有理数立方和的整数比例：

9.5%~83%。

所以这一范围究竟是怎么得出的？

如何圈定这一范围？

正如上面所说，椭圆曲线的结构极其复杂，这也使得它的直接求解变得非常困难。

于是这3位数学家开始思考：为何不试试将它与更容易处理的东西联系起来呢？这一想就想到了矩阵。

这3位数学家中的1位，曾在今年4月证明过一个理论：

如果一个立方和方程存在有理数解（rational solutions），那么至少存在一个2×2×2×2的四维矩阵与它对应。

依据这个理论，如果能想办法计算出整数的2个分数立方和方程是否有对应的四维矩阵，就有办法求解出不可能被表示成有理数立方和的整数范围。

具体的求解过程，涉及两方面的理论：

一部分是几何数论，涉及计算不同几何图形在坐标系中的格点（lattice points）；另一部分则是解析数论，与哈代-李特尔伍德圆法（定理）相关。

最终他们求解出的结果是，大约有1/6的整数不存在对应的四维矩阵，换言之，这1/6的整数完全不可能被表示成2个有理数立方和的形式。

这样就确定了这个范围的最大上限——至多有5/6（约83%）的整数可能被表示成有理数立方和。

所以求解下限的话，将定理反过来不就行了？

并非如此。毕竟这个理论的逆定理并没有被证明成立，即“如果一个整数能找到对应的四维矩阵，则它也能被表示为2个有理数的立方和”。

为此，三位数学家求助了椭圆曲线领域中对逆定理颇有研究的2位专家，分别是来自德克萨斯大学奥斯汀分校的Ashay Burungale和普林斯顿大学的Christopher Skinner。

他们一番捣鼓后，给出了一个特殊情况下逆定理成立的条件，在这种情况下至少存在2/21的整数，能表示为2个有理数的立方和。而2/21（约9.5%）这个数值，也正是这一整数范围的下限。

但毕竟是特殊情况，所以3位数学家认为，9.5%~83%这个整数范围还能被进一步缩小。接下来，他们打算进一步提升下限9.5%的数值，以接近逆定理完全成立下的5/12（约41%）。

领域内的学者认为，这一成果突破，表明数学家们距离贝赫和斯维讷通-戴尔猜想的证明又前进了一大步。

作者之一为菲尔兹奖得主

这次研究之前，3位数学家已经在数论领域有过几次合作了。

其中，Ari Shnidman和Manjul Bhargava早在2012年就有过数论领域的合作，而Manjul Bhargava又是Levent Alpöge在普林斯顿大学读博期间的导师。

Levent Alpöge，哈佛大学初级研究员，本科毕业于哈佛大学数学系，并获得了物理系硕士学位，随后他获得普林斯顿大学数学系的硕士、博士学位。

他曾于2015年获得摩根奖，这个奖项每年颁给数学研究出色的大学生。

Ari Shnidman，以色列希伯来大学数学系的高级讲师，研究兴趣是包括算数统计学、算数几何等在内的数论方向。

Manjul Bhargava，普林斯顿大学数学系教授，本科毕业于哈佛大学，博士毕业于普林斯顿大学，研究方向是几何数论。

他于2014年获得菲尔兹奖，获奖理由是在几何数论领域做出的突出贡献，包括开辟新方法来计算“小”秩（“小”指最多不超过5）的环数和估计椭圆曲线平均秩的界等。

值得一提的是，其中他研究的关于“椭圆曲线三次方程的有理数解”也是获奖原因之一，这次研究的两个有理数的立方和问题，就是其中的一种特殊求解情况。

这次突破有不少理论基础，就建立在Manjul Bhargava之前做过的工作上。

论文地址：https://arxiv.org/abs/2210.10730

参考链接

[1]https://www.quantamagazine.org/mathematical-trio-advances-centuries-old-number-theory-problem-20221129/

[2]https://swc-math.github.io/aws/2009/09BhargavaNotes.pdf[3]http://math.huji.ac.il/~shnidman/

本文来自微信公众号：量子位 （ID：QbitAI），作者：Pine、萧箫