这个险值得冒吗？

本文摘选自《你的答案有多正确？像数学家一样思考》，作者：Anne Rooney（安妮·鲁尼），译者：杨万东、朱雨秋、朱鸿飞，出版：中译出版社，头图来自：《赌博默示录》

我们对风险的感知非常奇怪，而且我们的感知并不总是很理智地与风险数据相关。它受到许多心理因素影响，如熟悉或新奇、（关于风险的）未知因素、我们感觉自己具备的控制水平、结果的稀缺性、避免风险带来的不便、危险的紧迫性以及它可以造成的伤害程度。

刀口舐血！

从逻辑上来说，如果一项活动伴随着相对高的死亡率或重伤风险，我们似乎会避开它——然而许多人还是会开快车、抽烟、暴饮暴食。

2014—2015 年埃博拉病毒爆发。

埃博拉拥有一种骇人风险的所有特征：

1. 感染伴随着逾 50% 的死亡率；

2. 症状令人毛骨悚然；

3. 大多数人都不熟悉它；

4. 大范围的媒体报道；

5. 人们感觉疾病不受控制，因为它的侵袭很随意（尽管还没随意到会感染 5,000 千米外的某个人）。

另外还有大量未知因素。

埃博拉会逸出非洲吗？它会在出现症状前在人际传播吗？然而为避免这个风险而导致的不便相当轻微：不要去非洲，不要在埃博拉医院周围逗留或处理尸体。多数人会在没有任何重大危险或招致许多不便的情况下害怕埃博拉。

坐汽车也是一种已知风险。我们熟悉它，感觉它在我们的控制中，即使那种感觉在某种程度上是错觉（我们控制不了其他司机）。当然，媒体上少有交通事故的报道，因为它们太常见了，这一点也表明了很高程度的风险。大部分人不怕坐汽车，而且不坐汽车也非常不方便。

很吓人，但风险低

对人类最致命的动物并不像你想象的那样是鲨鱼、老虎、河马或任何别的大型动物，连狗都不算。是蚊子。通过疟疾和其他疾病，蚊子每年杀死逾 50万人。然而大多数人会认为，在巴西的河岸边散步比在鲨鱼出没的澳大利亚沿海游泳更安全。淹死的概率比被鲨鱼咬死大 3,300 倍，因此如果你在水里活得够久，连鲨鱼都能看到，你可以算得上幸运了。

放上数字

与大部分数字类似，显示风险的数字必须放在特定的语境下才有意义。下面是两个与美国道路交通死亡有关的数字：

1950 年，33,186 人死于交通事故；

2013 年， 32,719 人死于交通事故

乍一看，似乎从 1950 年以来，道路安全方面没什么进步。这个想法令人沮丧。但加上更多信息有助于更好地理解这些数字。如果我们看看不同时期的美国人口，我们可以更清楚地看到实际情况。1950 年，美国人口约为 1.52 亿；但 2013 年，这个数字是 3.16 亿，翻倍还不止。

如果我们用人口数除以死亡人数，进步似乎很明确：

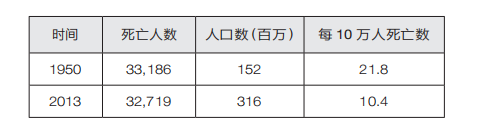
但如果我们看看这两年乘机动车旅行的英里数，这些数字呈现出完全不同的情况。

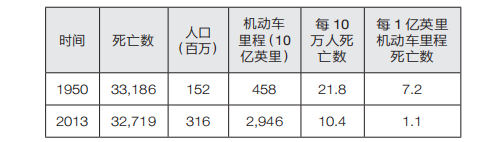
在 1950 年乘车的危险程度是 2013 年的 7 倍，后者的风险降低了 85%。

百万分之一

风险分析师将百万分之一的死亡机会称作“百万分之一致死率”（a micromort）。如果你正在考虑如何去镇上或去上班，你可以比较不同交通工具的风险，用“百万分之一致死率”来计算你需要旅行多少千米才可能死于一场事故。

显然，坐火车是最安全的方式，骑摩托车是最危险的方式。

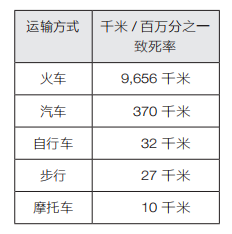
长期风险与急性风险

从楼梯上摔下，折断脖子的风险是急性风险——它可能即时发生并且立即要了你的命。如果你安全地走下楼梯，风险（暂时）消失，而你除了也许有过一点点担心外，没受到任何有害影响。

抽烟导致肺癌的风险是长期风险。它随着时间累积，尽管你今天下午可能抽的任何一支烟都不会杀死你，它可能（与所有其他烟一起）促成更短的寿命。这种风险是累积的，你抽的每支烟都会增加你得肺癌和其他疾病的风险。

百万分之一生命与百万分之一致死率与百万分之一致死率相对的是“百万分之一生命”（a microlife）——生命的一百万分之一。对一个年轻成人而言，这平均约等于半个小时。长期风险常常更适合用百万分之一生命的代价来表示。抽支烟消耗掉约1个百万分之一生命。当然，它不是直接和无可争议的代价，而是一种风险。

如果抽取特定数量香烟的人的平均寿命，将它与不抽烟者的平均寿命相比，我们可以算出一支烟平均消耗多少个百万分之一生命。但一些人 1 天抽 20支烟并且活到 90 岁；没什么事是确定的。

用百万分之一致死率来计算一种活动的急性风险与用百万分之一生命来计算长期风险的关键区别是，百万分之一生命的代价是累积的，而百万分之一致死率的风险则在你每次幸存后重置为零。

风险无处不在考查风险的另一个方式是将它与基线风险做比较，基线风险是你只要活着就会承担的风险。每参加一次悬挂滑翔飞行，死于这种运动的概率约为 1/116,000。一名 30 岁的美国男性在任意一天死去的概率为 1/240,000，因此参加悬挂滑翔使他的风险增大到原来的 3 倍（因为他将新风险加到现存风险上，而不是取代它）。

表达风险的另一个方式是指出你需要连续从事一项活动多久才会出事，或计算一种活动每从事一次所冒的风险。如果每次悬挂滑翔飞行的死亡风险是 1/116,000，那意味着如果你准备悬挂滑翔 116,000 次，你很有可能死于其中某一次（尽管它可能是在你第 3 次或第 169 次，而不是第 116,000 次飞行中）。虽然在平均水平上是这样，但对任何特定的人则不一定如此。

发挥作用的还可能有其他因素。刚开始参加悬挂滑翔飞行也许因为飞行员经验不足而更加危险，后来的飞行也许因为飞行员厌烦了而更加危险。某个悬挂滑行飞行员也许比别人经验更多或更少，因而危险更大或更小。

邮政编码里的运气

保险公司会尝试更准确地评估犯罪或意外事件的风险，而不是仅仅满足于采用全部人口的平均数据。他们用非常复杂的方法计算出谁比别人的危险更大或更小。

这就是你的邮政编码会影响你需要为房屋保险、汽车保险等支付多少的原因。如果你所在地区有大量的入室劫案，他们会评估你的屋子遭到非法闯入的风险较高，向你收取更高的保费。

增加的风险与减少的风险指示风险的一个常见方式是用倍数或百分比的形式对它们做比较。这可以很有说服力，但如果我们看不到任何绝对数，也很容易受到误导。一个像“服用保健药让你得脚趾恶性黑色素瘤的风险降低一半”这样的说法让这种补剂听上去物有所值。但如果得脚趾恶性黑色素瘤的概率仅有 2,000 万分之一，花钱买保健药将这个风险降一半到 4,000 万分之一其实是不值的。

相比得脚趾恶性黑色素瘤，你更有可能在去买这种补药的路上出事故。

一些风险没法用我们喜欢的准确程度来衡量。如果我们尝试根据你过去的经验来预测你死于交通事故的风险，这个概率将会是零，因为尽管你在路上许多年，但从未死于交通事故。

对风险的误解有两种常见做法，总结起来就是类似下面的说法：

“多少年来，我一直在这样做，从来没出过问题，因此我确定以后还是没问题。”

“到目前为止你都很幸运，但运气肯定会用完。”

在某种意义上，第一个说法是一种不明确的贝叶斯概率评估。如果我们不知道一种风险的统计数据，我们会根据既往例子做出评估。不过这不是个好主意，尤其是在与死亡风险打交道的时候。

当然，你在以前的情形下一直没问题，因为你还没死。你在之前的情形下没死，你绝对可以用那些情形为任何鲁莽的举动辩护，因为你从没有死于之前的任何冒险举动。你这次死不了，因为你上次没死。但仅仅因为上一次没死，你就可能死于这一次。

第二个说法在许多情况下也是错的。这是赌徒因为某个数字迟早会出现而一直押它的做法的反面。但情况不是那样。不管一种情况之前是否出现过，它每次出现的概率都是一样的。如果你掷一个骰子，得到 6 点的机会是 1/6。如果你投出一个 6 点，下次投出 6 点的概率还是 1/6。因此在独立风险的情况下，某人多年来“全身而退”的事实并不意味着他们会（或不会）继续全身而退。

作者: Anne Rooney（安妮·鲁尼）

出版社: 中译出版社

译者: 杨万东 / 朱雨秋 / 朱鸿飞

出版年: 2022-3

本文摘选自《你的答案有多正确？像数学家一样思考》，作者：Anne Rooney（安妮·鲁尼），译者：杨万东、朱雨秋、朱鸿飞，出版：中译出版社